本试题 “如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A 和B ,在各自不同的水平面做匀速圆周运动,以下说法正确的是[ ]A.VA>VBB.ωA>ωB C.aA>aB...” 主要考查您对线速度
角速度
向心加速度
向心力
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 线速度
- 角速度
- 向心加速度
- 向心力
线速度的定义:
质点沿圆周运动通过的弧长与所用时间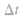 的比值叫做线速度。
的比值叫做线速度。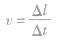 ,
,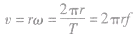 。
。
线速度的特性:
线速度是矢量,方向和半径垂直,和圆周相切。它是描述做圆周运动的物理运动快慢的物理量。
对线速度的理解:
物体上任一点对定轴作圆周运动时的速度称为“线速度”。它的一般定义是质点作曲线运动时所具有的顺时速度。它的方向沿运动轨道的切线方向,故又称切向速度。它是描述作曲线运动的质点运动快慢和方向的物理量。物体上各点作曲线运动时所具有的顺时速度,其方向沿运动轨道的切线方向。 (高中物理中的切线方向就指速度一侧的方向,和数学中的切线不同)
知识点拨:
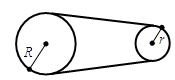
如图,大圆和小圆有同一根皮带相连,皮带上的各个点的速率相同,所以大圆和小圆圆周上的线速度是相同的。
角速度的定义:
圆周运动中,连接质点和圆心的半径转过的角度 跟所用时间
跟所用时间 的比值叫做角速度。
的比值叫做角速度。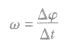 ,
,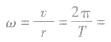
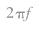 。
。
角速度的特性:
角速度是矢量,高中阶段不研究其方向。它是描述做圆周运动的物体绕圆心转动快慢的物理量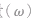 。
。
单位:在国际单位制中,单位是“弧度/秒”(rad/s)。(1rad=360d°/(2π)≈57°17'45″)
转动周数时(例如:每分钟转动周数),则以转速来描述转动速度快慢。角速度的方向垂直于转动平面,可通过右手螺旋定则来确定。(角速度的方向,在高中物理的学习不属于考察的内容)
线速度和角速度的对比:
角速度是单位时间转过的角度;或者说是转过的角度和所用时间的比值。
线速度是单位时间走过的弧长;或者说是弧长和所用时间的比值。
角速度和线速度的关系:
知识拓展提升:
例:计算地球和月亮公转的角速度:

通过计算知道,书中所提到的地球和月球的争论是没有结论的。比较运动得快慢,要看比较线速度还是角速度,不能简单说谁快谁慢。
向心加速度的定义:
描述线速度方向变化的快慢,大小![]() ,方向总是指向圆心,但时刻在变化,是一个变加速度。
,方向总是指向圆心,但时刻在变化,是一个变加速度。
向心加速度的特性: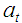 切向加速度,作用是改变速度的大小,
切向加速度,作用是改变速度的大小, 法向加速度
法向加速度
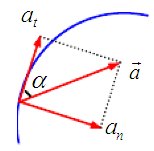
所以,当只有法向加速度的时候,物体将做匀速圆周运动。
知识点拨:
向心力的作用效果:产生向心加速度,只改变线速度的方向,不改变速度的大小.因此,向心力不做功.
向心力总是指向圆心方向的。
知识拓展:
向心力,可以是几个力的合力,也可以是某个力的一个分力;既可能是重力、弹力、摩擦力,也可能是电场力、磁场力或其他性质的力。如果物体做匀速圆周运动,则所受合力一定全部用来提供向心力。
向心力的定义:
在圆周运动中产生向心加速度的力。![]() 。
。
向心力的特性:
1、向心力
总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小,大小![]() ,方向总是指向圆心(与线速度方向垂直),方向时刻在变化,是一个变力。向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供。
,方向总是指向圆心(与线速度方向垂直),方向时刻在变化,是一个变力。向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供。
2、轻绳模型
Ⅰ、轻绳模型的特点:
①轻绳的质量和重力不计;
②可以任意弯曲,伸长形变不计,只能产生和承受沿绳方向的拉力;
③轻绳拉力的变化不需要时间,具有突变性。
Ⅱ、轻绳模型在圆周运动中的应用
小球在绳的拉力作用下在竖直平面内做圆周运动的临界问题:
①临界条件:小球通过最高点,绳子对小球刚好没有力的作用,由重力提供向心力:
②小球能通过最高点的条件: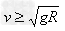 (当时
(当时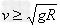 ,绳子对球产生拉力)
,绳子对球产生拉力)
③不能通过最高点的条件: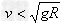 (实际上小球还没有到最高点时,就脱离了轨道)
(实际上小球还没有到最高点时,就脱离了轨道)
3、轻杆模型:
Ⅰ、轻杆模型的特点:
①轻杆的质量和重力不计;
②任意方向的形变不计,只能产生和承受各方向的拉力和压力;
③轻杆拉力和压力的变化不需要时间,具有突变性。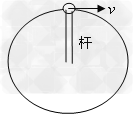
Ⅱ、轻杆模型在圆周运动中的应用
轻杆的一端连着一个小球在竖直平面内做圆周运动,小球通过最高点时,轻杆对小球产生弹力的情况:
①小球能通过最高点的临界条件: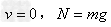 (N为支持力)
(N为支持力)
②当时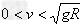 ,有
,有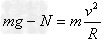 (N为支持力)
(N为支持力)
③当时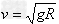 ,有
,有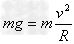 (N=0)
(N=0)
④当时 ,有
,有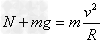 (N为拉力)
(N为拉力)
知识点拨:
向心力是从力的作用效果来命名的,因为它产生指向圆心的加速度,所以称它为向心力。它不是具有确定性质的某种类型的力。相反,任何性质的力都可以作为向心力。实际上它可是某种性质的一个力,或某个力的分力,还可以是几个不同性质的力沿着半径指向圆心的合外力。对一个物体进行受力分析的时候,是不需要画向心力的,向心力是效果力。
知识拓展:
对于向心力的理解,同学们可以切身的体会一下。两个同学手拉手,甲同学原地,乙同学绕着甲同学转,甲同学给乙同学的拉力就是向心力,当拉力大于向心力的时候,乙同学向心(甲同学)运动,当拉力小于向心力的时候,乙同学做离心运动。
与“如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相...”考查相似的试题有:
- 某机器内有两个围绕各自固定轴匀速转动的铝盘A、B,A盘上固定一个信号发射装置P,能持续沿半径向外发射红外线,P到圆心的距离...
- 近年许多电视台推出户外有奖冲关的游戏节目,如图(俯视图)是某台设计的冲关活动中的一个环节.要求挑战者从平台上跳到以O为...
- 如图所示,内壁光滑的圆台形容器固定不动,其轴线沿竖直方向.使一小球先后在M和N两处紧贴着容器内壁分别在图中虚线所示的水...
- 如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮上质量相等的两个质点,则偏心轮转动过程中a、b两质点[ ]A.角速度大小...
- 物体做匀速圆周运动,下列关于它的周期正确的说法是( ) A.物体的线速度越大,它的周期越小 B.物体的角速度越大,它的周期...
- 如图所示,是A、B两物体做匀速圆周运动时的向心加速度随半径变化的关系图象,A是以坐标轴为渐近线的双曲线,B是一条过原点的...
- 如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线,表示质点P的图线是双曲线,表示Q的图线是过原点的一条直线...
- 如图所示,质量不计的光滑直杆AB的A端固定一个小球P,杆OB段套着小球Q,Q与轻质弹簧的一端相连,弹簧的另一端固定在O点,弹簧...
- 如图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为2L,B处绳长为L,两根绳能承受的最大...
- 如图所示,V形细杆AOB能绕其对称轴OO′转动,OO′沿竖直方向,V形杆的两臂与转轴间的夹角均为α=45°.两质量均为m=0.1kg的小环,...