本试题 “如图所示,在一直立的光滑管内放置一轻质弹簧,弹簧上端O点与管口A的距离为2x0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空...” 主要考查您对弹力的大小、胡克定律
能量转化与守恒定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 弹力的大小、胡克定律
- 能量转化与守恒定律
弹力的大小:
弹力的大小与物体的形变程度有关,形变量越大,产生的弹力越大;形变量越小,产生的弹力越小。
(1)一般情况下,弹力的大小可以利用平衡条件或牛顿运动定律计算出来;对于弹簧的弹力,在弹性限度内遵循胡克定律:
(2)胡克定律在弹性限度内,弹簧的弹力和其形变量(伸长或缩短的长度)成正比,即F=kx,式中k为劲度系数,x为弹簧的形变量,F为弹力。
胡克定律的图像如图所示。 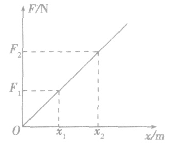
①式中形变量是指在弹性限度内发生的。形变量x是弹簧在原长基础上的改变量,即弹簧伸缩后的长度L与原长L0的差:x=|L—L0|,不能将x当做弹簧的长度。
②胡克定律中劲度系数k的单位是N/m,由弹簧自身的条件(材料、长度、横截面积)决定,弹簧做好后,劲度系数是确定的。不同弹簧的劲度系数一般不同。
③劲度系数k的两种求法
a.由胡克定律F=kx知:k=F/x
b.由F一x图像知: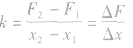
判定弹力的有无及其方向的方法:
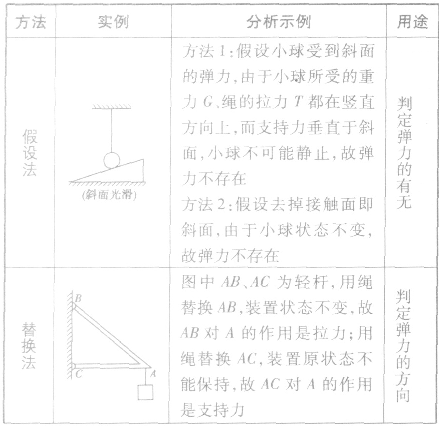
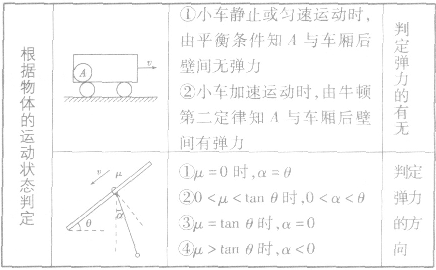
能量守恒定律:
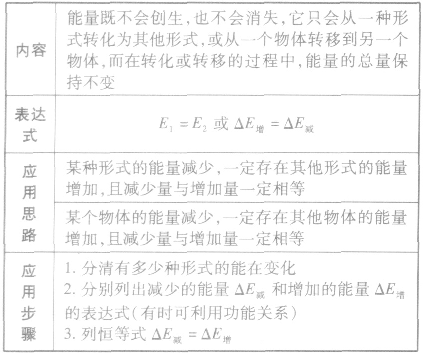
能量守恒中连接体问题的解法:
在两个或两个以上的物体组成的系统中,单独研究其中一个物体时,机械能往往是不守恒的,但对整体来说,机械能又常常是守恒的,所以在这类问题中通常需取整体作为研究对象,再找出其他运动联系来解题。
在判断系统的机械能是否守恒时,除重力、弹力外无其他外力做功,只是系统机械能守恒的必要条件,还需要看系统内力做功的情况。
(1)系统内两个直接接触的物体,如果满足动量守恒和机械能守恒条件,利用两守恒定律是解这类问题的常用方法两物体的运动联系是沿垂直于接触面的分速度相等。
(2)以轻绳相连的两个物体,如果和外界不存在摩擦力做功等问题时,只有机械能在两个物体之间的相互转移,两物体系统机械能守恒。解此类问题的关键是在绳的方向上两物体速度大小相等。
(3)与轻杆相连的物体在绕固定转动轴转动时,两物体的角速度相等。无转动轴时两物体沿杆方向的分速度相等。有摩擦阻力参与过程的能量问题的解法在有摩擦力或介质阻力参与的过程中,机械能不停地向内能转化,但在摩擦力或介质阻力大小不变的情况下,损失的机械能与通过的路程成正比。而在往返运动形式中,通过同一位置时的速率也就不相同,通过同样距离所用时间也不相同。在比较运动时间时,可以通过比较平均速度的大小进而得到时间关系。
与“如图所示,在一直立的光滑管内放置一轻质弹簧,弹簧上端O点与...”考查相似的试题有:
- 关于力说法下列正确的是( )A.匀速转弯的物体一定受到力的作用B.物体发生形变后必然会产生弹力C.物体先受到外力发生形变...
- 白云山风景区内有一种叫做“蹦极跳”的运动中,质量为m的游戏者身系一根长为L、弹性优良的轻质柔软的橡皮绳,从高处由静止开始...
- 关于弹力,下列说法中正确的是 ( )A.物体只要相互接触就有弹力作用B.物体只要发生了形变就有弹力作用C.弹力产生在直接接触...
- 如图所示,一根弹簧的原长为20cm,竖直悬挂着,当用15N的力竖直向下拉弹簧时,量得弹簧长24cm;若把它竖立在水平桌面上,用30...
- 如图所示,水平固定倾角为30°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,重力加速度为g.现...
- 质量为5.0103kg的物体,在高空受到的重力为4.8104N,该处的重力加速度g= m/s2。如果该处有另一质量为5kg的物体,放在竖直放置...
- 如图所示,轻弹簧一端竖直固定在水平地面上,其正上方有一个物块,物块从高处自由下落到弹簧的上端O处,将弹簧压缩了x0时,物...
- 如图所示,图甲是某同学自制的电子秤原理示意图.目的是利用理想电压表的示数指示物体的质量.托盘与电阻可忽略的金属弹簧相...
- 关于摩擦力与弹力的关系,下列说法中不正确的是A.接触面间有摩擦力就一定有弹力B.接触面间有弹力但不一定有摩擦力C.摩擦力...
- 在2008年北京奥运会上,俄罗斯著名撑杆跳运动员伊辛巴耶娃以5.05m的成绩第24次打破世界纪录.图为她在比赛中的几个画面,下列...