本试题 “如图甲是某电场中的一条电场线,A、B是这条线上的两点,一带负电的微粒只受电场力作用,从静止开始沿电场线从A运动到B。在这过程中,电荷的速度一时间图线如...” 主要考查您对电场强度的定义式
电势能
电势
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 电场强度的定义式
- 电势能
- 电势
电场强度:


计算场强的四种方法:
1.计算电场强度的常用方法——公式法
(1)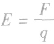 是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
(2)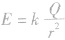 要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
(3)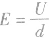 是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
2.计算多个电荷形成的电场强度的方法——叠加法
当空间的电场由几个点电荷共同激发的时候,空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和,其合成遵循矢量合成的平行四边形定则。
3.计算特殊带电体产生的电场强度的方法
(1)补偿法对于某些物理问题,当直接去解待求的A很困难或没有条件求解时,可设法补上一个B,补偿的原则是使A+B成为一个完整的模型,从而使A+B变得易于求解,而且,补上去的B也必须容易求解。这样,待求的A便可从两者的差值中获得,问题就迎刃而解了,这就是解物理题时常用的补偿法。用这个方法可算出一些特殊的带电体所产生的电场强度。
(2)微元法在某些问题中,场源带电体的形状特殊,不能直接求解场源带电体在空间某点所产生的总电场,此时可将场源带电体分割,在高中阶段,这类问题中分割后的微元常有部分微元关于待求点对称,这就可以利用场的叠加及对称性来解题。
4.计算感应电荷产生的电场强度的常用方法—— 静电平衡法根据静电平衡时导体内部场强处处为零的特点,外部场强与感应电荷产生的场强(附加电场)的合场强为零,可知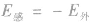 ,这样就可以把复杂问题变简单了。
,这样就可以把复杂问题变简单了。
电势能:
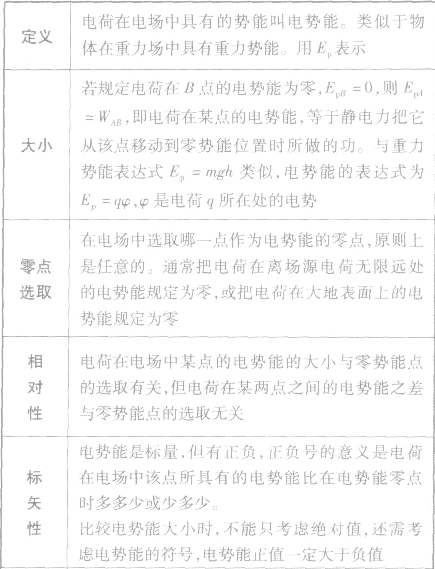

电势能大小的比较方法:
1.由公式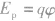 判断
判断
设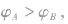 当
当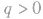 时,
时,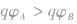 ,即
,即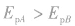 ;当
;当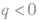 时,
时, 可总结为正电荷在电势高的地方电势能大,而负电荷在电势高的地方电势能小。
可总结为正电荷在电势高的地方电势能大,而负电荷在电势高的地方电势能小。
2.做功判断法电场力做正功,电荷(无论是正电荷还是负电荷) 从电势能较大的地方移向电势能较小的地方。反之,如果电荷克服电场力做功,那么电荷将从电势能较小的地方移向电势能较大的地方。
1、电势φ:电场中某点的电势等于该点相对零电势点的电势差。
2、特点:
①电势具有相对性,相对参考点而言。但电势之差与参考点的选择无关。通常取离电场无穷远处或大地的电势为零电势。
②电势一个标量,但是它有正负,正负只表示该点电势比参考点电势高,还是低。
③电势的大小由电场本身决定,与Ep和q无关。
④电势在数值上等于单位正电荷由该点移动到零势点时电场力所做的功。
3、电势高低的判断方法
①根据电场线判断:沿着电场线的方向,电势越来越低。
②根据电势能判断:
正电荷:电势能大,电势高;电势能小,电势低。
负电荷:电势能大,电势低;电势能小,电势高。
结论:只在电场力作用下,静止的电荷从电势能高的地方向电势能低的地方运动。
电场的能的性质:
电场力做功的特点在电场中移动电荷时,电场力对电荷做的功只与电荷的起始位置和终止位置有关,而与电荷的运动路径无关。这一点与重力做功的情况类似。沿任一闭合路径移动一周,电场力所做的总功为零。
电势高低的比较方法:
(1)根据电场线或等势面判断。沿电场线方向,电势越来越低,电场线由电势高的等势面指向电势低的等势面。
(2)利用电势差的正负判断。判断出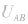 的正负,再由
的正负,再由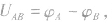 比较
比较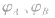 的大小。若
的大小。若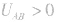 ,则
,则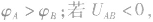 ;则
;则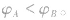
(3)利用场源电荷判断。取无穷远处为零电势点,正电荷周围电势为正值,且离正电荷近处电势高;负电荷周围电势为负值,且离负电荷近处电势低。点电荷电场中某固定点的电势与场源电荷的电性及电荷量有关。场源电荷带正电时,电荷量越大.该点电势越高;场源电荷带负电时则相反。
(4)利用电势叠加判断。苦有多个场源电荷时,每个场源电荷产生的电场中的电势已知或易于判断,可将每个电场的电势先判断后叠加从而得到总电势。
(5)根据电场力做功来判断。正电荷在电场力作用下移动时,电场力做正功,电荷由高电势处移向低电势处;正电荷克服电场力做功,电荷由低电势处移向高电势处。对于负电荷,情况正好相反。
(6)根据电势能判断。正电荷在电势高处电势能较大,负电荷在电势低处电势能较大。
与“如图甲是某电场中的一条电场线,A、B是这条线上的两点,一带...”考查相似的试题有:
- 在电场中某点放一电量为q的试探电荷,所受电场力大小为F,根据场强定义可知,该点的场强大小E=F/q。下列说法正确的是( )A....
- 不定项选择以下说法正确的是( )A.由公式E=可知,场强E跟电荷所受电场力成正比,跟电荷量成反比B.公式E=只适用于匀强电场C....
- 如图所示,真空中存在范围足够大的匀强电场,A、B为匀强电场的两个等势面。现有三个完全相同的带等量正电荷的小球a、b、c,从...
- 如图所示,虚线以a、b、c表示在O处某一点电荷的电场中的三个等势面,设两相邻等势面的间距相等.一电子射入电场后的运动轨迹...
- 位于A、B处的两个带有不等量负电的点电荷在平面内电势分布如图所示,图中实线表示等势线,则[ ]A.a点和b点的电场强度相同B....
- 一个电子只在电场力作用下从a点运动到b点,轨迹如图中虚线所示,图中的一组平行实线表示的可能是电场线也可能是等势面,则下...
- 下列关于电势和电势能的说法中正确的是[ ]A.克服电场力做功时,电荷的电势能减少B.电荷在电场中某点的电势能与其电荷量的比...
- 不定项选择A、B在两个等量异种点电荷连线的中垂线上,且到连线的距离相等,如图所示,则( )A.同一点电荷在A、B两点的电势...
- 空间某一静电场的电势在轴上分布如图所示,轴上两点B、C点电场强度在方向上的分量分别是、,下列说法中正确的有[ ]A.的方向...
- 如图所示,a、b是竖直方向上d电场线d两点,一带电质点在a点由静止释放,沿电场线向上运动,到b点恰好速度为零,下列说法中正...