本试题 “一质量为M=0.8 kg的中空的、粗细均匀的、足够长的绝缘细管,其内表面粗糙、外表面光滑;有一质量为m=0.2 kg,电荷量为q=0.1 C的带正电小滑块以水平向右的速度...” 主要考查您对动量守恒定律的应用
磁场对运动电荷的作用:洛伦兹力、左手定则
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动量守恒定律的应用
- 磁场对运动电荷的作用:洛伦兹力、左手定则
1、动量守恒定律:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。即m1v1+m2v2=m1v1'+m2v2'。
2、动量守恒定律的常见问题:
①碰撞问题;
②爆炸问题;
③反冲现象;
④人船模型;
“人船模型”是动量守恒定律的应用的一个经典模型,该模型应用的条件:一个原来处于静止状态的系统,当系统中的物体间发生相对运动的过程中,有一个方向上动量守恒。
⑤子弹打木块模型。
子弹打木块模型及推广:
Ⅰ、一物块在木板上滑动,μNS相对=ΔEk系统=Q,Q为摩擦在系统中产生的热量;
Ⅱ、小球在置于光滑水平面上的竖直平面内弧形光滑轨道上滑动,包括小车上悬一单摆单摆的摆动过程等。小球上升到最高点时系统有共同速度(或有共同的水平速度);系统内弹力做功时,不将机械能转化为其它形式的能,因此过程中系统机械能守恒。
Ⅲ、一静一动的同种电荷追碰运动等。
从“六性”把握动量守恒定律的应用方法:
1.条件性
动量守恒定律的成立是有条件的,只有当系统满足动量守恒的条件时才能利用方程式进行计算。
2.矢量性
动量守恒方程是一个矢量方程。对于作用前后物体的运动方向都在同一直线上的问题,应选取统一的正方向,凡是与选取正方向相同的动量为正,相反为负。若方向未知,可设为与正方向相同列动量守恒方程,通过解得结果的正负,判定未知量的方向。
3.参考系的同一性速度
具有相对性,公式中的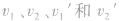 均应对同一参考系而言,一般均取对地的速度。
均应对同一参考系而言,一般均取对地的速度。
4.状态的同一性
相互作用前的总动量,这个“前”是指相互作用前的某一时刻,所以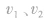 均是此时刻的瞬时速度,同理
均是此时刻的瞬时速度,同理 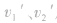 应是相互作用后的某一时刻的瞬时速度。
应是相互作用后的某一时刻的瞬时速度。
5.整体性
动量守恒定律是针对一个物体系统而言的,具有系统的整体性。
6.普适性
它不仅适用于两个物体所组成的系统,也适用于多个物体组成的系统;不仅适用于宏观物体组成的系统,也适用于微观粒子组成的系统。
临界与极值问题的解法:
在动量守恒定律的应用中,常常会遇到相互作用的两物体相距最近、避免相碰和物体开始反向运动等临界问题。分析临界问题的关键是寻找临界状态,临界状态的出现是有条件的,这种条件就是临界条件。临界条件往往表现为某个(或某些)物理量的特定取值。在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,这些特定关系的判断是求解这类问题的关键。
“人船模型”的解题规律:
“人船模型”是动量守恒定律的拓展应用,它把速度和质量的关系推广到质量和位移的关系,这样给我们提供了一种解题思路和解决问题的方法。人船问题的适用条件是:两个物体组成的系统(当有多个物体组成系统时,可以先转化为两个物体组成的系统)动量守恒,系统的合动量为零。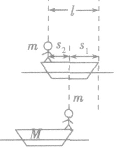
这种模型中涉及两种题型,一种题型是求解某物体在相互作用过程中通过的位移,此题型中需根据动量守恒、位移关系得到两个关系求解,如在图中,人从船头走到船尾时由动量守恒可得: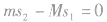
再由图中几何关系有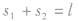
可得人船的位移分别为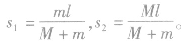
另一种题型是求某一时刻物体的速度,这种题型是先要由动量守恒求得两物体的一个速度关系,再由能量守恒得到两物体的另一个速度关系,从而求得物体的瞬时速度(或与瞬时速度相关的物理量)。
安培力与洛伦兹力:
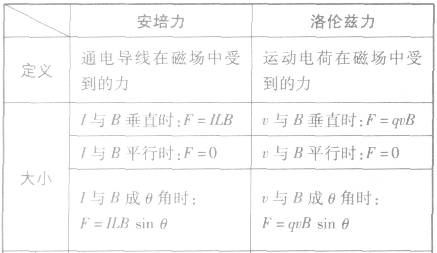

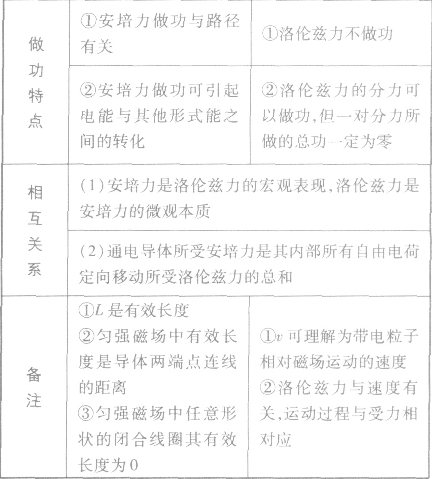
洛伦兹力作用下力学问题的解决方法:
(1)涉及洛伦兹力的动力学问题中,因洛伦兹力的大小和方向与物体的运动状态有关,在分析物体的运动过程时,需将运动对受力的影响、受力对运动的影响综合考虑来确定物体的运动性质及运动过程,此类问题中往往还会出现临界状态,需分析临界状态下满足的条件。
(2)在涉及洛伦兹力的能量问题中,因洛伦兹力不做功,系统能量的转化取决于其他力做功的情况,但需考虑洛伦兹力对最终运动状态的影响。
(3)在定性判定涉及洛伦兹力的非匀变速运动过程中,可利用运动的合成与分解来定性地判定通过的位移、运动的时间等问题。
与“一质量为M=0.8 kg的中空的、粗细均匀的、足够长的绝缘细管,...”考查相似的试题有:
- 如图所示,平板小车A放置于光滑水平面上,小滑块B以初速度v0=8m/s滑上平板小车左端,当B从小车右端滑出时,小车A的速度为1m/s...
- 如图所示,在光滑的水平面上有一物体M,物体上有一光滑的半圆弧轨道,最低点为C,两端A、B一样高。现让小滑块m从A点静止下滑...
- 如图所示,质量为2 kg的物体A以4 m/s的速度在光滑水平面上自右向左运动,一颗质量为20 g的子弹以500 m/s的速度自左向右穿过A...
- 如图所示,在光滑的水平面上,有一质量M=3 kg的薄板和一质量m=1kg的物块朝相反方向运动,初速度大小都为v=4 m/s,它们之间有...
- 质量为m,电荷量为q的带电粒子以速率v垂直射入磁感强度为B的匀强磁场中,在磁场力作用下做匀速圆周运动,带电粒子在圆形轨道...
- 如图所示,a、b两平行金属板置于匀强磁场中,一束电子从上而下从a、b两板间通过,由于磁场的作用,则A.板左侧聚集较多的电子...
- 电量相同质量不同的同位素离子以相同的速率从a孔射入正方形空腔中,空腔内匀强磁场的磁感应强度方向如图所示.如果从b、c射出...
- 如图所示,在加有匀强磁场的区域中,一垂直于磁场方向射入的带电粒子轨迹如图所示,由于带电粒子与沿途的气体分子发生碰撞,...
- 如图所示,接通开关S的瞬间,用丝线悬挂于一点可自由转动的通电直导线AB将( )A.A端向上,B端向下,悬线张力不变B.A端向下,...
- (5分)如图所示,在x轴的上方(y≥0)存在着垂直于纸面向外的匀强磁场,磁感应强度为B.在原点O有一个离子源向x轴上方的各个方向发...