本试题 “如图所示,光滑绝缘的水平面上,相隔2L的A、B两点固定有两个电荷量均为Q的正点电荷,aOb是AB连线上的三点,且O为中点,Oa=Ob=L/2,一质量为m、电荷量为q的点...” 主要考查您对动能定理
能量转化与守恒定律
点电荷的电场强度
电势
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动能定理
- 能量转化与守恒定律
- 点电荷的电场强度
- 电势
动能定理:
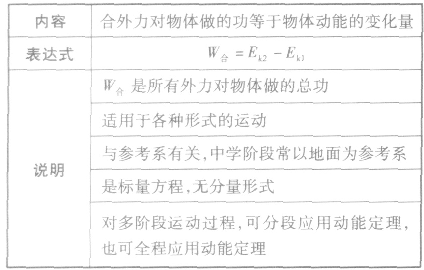
动能定理的应用方法技巧:
1.应用动能定理解题的基本思路
(1)选取研究对象,明确并分析运动过程。
(2)分析受力及各力做功的情况,求出总功:
(3)明确过程始、末状态的动能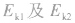 。
。
(4)列方程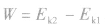 ,必要时注意分析题目潜在的条件,列辅助方程进行求解。
,必要时注意分析题目潜在的条件,列辅助方程进行求解。
2.应用动能定理应注意的几个问题
(1)明确研究对象和研究过程,找出始末状态的速度。
(2)要对物体正确地进行受力分析,明确各力做功的大小及正负情况(待求的功除外)。
(3)有些力在物体运动过程中不是始终存在的。若物体运动过程中包括几个阶段,物体在不同阶段内的受力情况不同,在考虑外力做功时需根据情况区分对待。
3.几种应用动能定理的典型情景
(1)应用动能定理求路程在多阶段或往返运动中,如果摩擦力或介质阻力大小不变,方向与速度方向关系恒相反,则在整个过程中克服摩擦力或介质阻力所做的功等于力与路程的乘积,从而可将物体在摩擦力或介质阻力作用下通过的路程与动能定理联系起来。
(2)应用动能定理求解多过程问题物体在某个运动过程中包含几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,但如能对整个过程根据动能定理列式求解,则可以使问题简化。根据题意灵活地选取研究过程,可以使问题变得简单。有时取全过程简单,有时取某一阶段简单。原则是尽量使做功的力减少,各个力的功计算方便,或使初、未动能等于零。
(3)用动能定理求变力的功变力的功无法用公式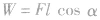 直接求解,有时该力也不是均匀变化的,无法用高中知识表达平均力,此时可以考虑用动能定理间接求解。涉及功、能的极值问题在涉及功、能的极值问题中,有些极值的形成是南运动形式的临界状态造成的。如竖直平面内圆周运动的最高点、平抛运动等。有些极值的形成是由题设条件造成的。在解决涉及功、能的极值问题时,一种思路是分析运动形式的临界状态,将临界条件转化为物理方程来求解;另一种思路是将运动过程的方程解析式化,利用数学方法求极值。
直接求解,有时该力也不是均匀变化的,无法用高中知识表达平均力,此时可以考虑用动能定理间接求解。涉及功、能的极值问题在涉及功、能的极值问题中,有些极值的形成是南运动形式的临界状态造成的。如竖直平面内圆周运动的最高点、平抛运动等。有些极值的形成是由题设条件造成的。在解决涉及功、能的极值问题时,一种思路是分析运动形式的临界状态,将临界条件转化为物理方程来求解;另一种思路是将运动过程的方程解析式化,利用数学方法求极值。
知识拓展:
1.总功的计算物体受到多个外力作用时,计算合外力的功,一般有如下三种方法:
(1)先由力的合成与分解法或根据牛顿第二定律求出合力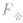 ,然后由
,然后由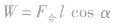 计算。采用此法计算合力的总功时,一是要求各力同时作用在物体上。二是要求合外力是恒力。
计算。采用此法计算合力的总功时,一是要求各力同时作用在物体上。二是要求合外力是恒力。
(2)由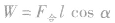 计算各个力对物体做的功
计算各个力对物体做的功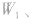
 ,然后将各个外力所做的功求代数和。当多阶段运动过程中不同阶段物体所受外力不同,即外力分阶段作用在物体上时常用此法求外力的总功。
,然后将各个外力所做的功求代数和。当多阶段运动过程中不同阶段物体所受外力不同,即外力分阶段作用在物体上时常用此法求外力的总功。
(3)外力做的总功等于物体动能的变化量,在物体初、末状态已知的情况下可考虑从动能变化量来确定合外力做的功。
2.系统动能定理
动能定理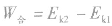 实质上是一个质点的功能关系,是针对单体或可看做单个物体的物体系而言的。所谓能看成单个物体的物体系,简单来说就是物体系内各物体之间的相对位置不变,从而物体系的各内力做功之和为零.物体系的动能变化就取决于所有外力做的总功了。
实质上是一个质点的功能关系,是针对单体或可看做单个物体的物体系而言的。所谓能看成单个物体的物体系,简单来说就是物体系内各物体之间的相对位置不变,从而物体系的各内力做功之和为零.物体系的动能变化就取决于所有外力做的总功了。
但是对于不能看成单个物体的物体系或不能看成质点的物体,可将其看成是由大量质点组成的质点系,对质点系组成的系统应用动能定理时,就不能仅考虑外力的作用,还需考虑内力所做的功。即: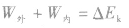
如人在从地面上竖直跳起的过程中,只受到了重力、地面支持力两个力的作用,而人从下蹲状态到离开地面的过程中,支持力不对人做功,重力对人做负功,但人的动能增加了,原因就在于此过程中人不能被看成单一的质点,人体内肌肉、骨骼之间的内力对人也做功。再如光滑水平面上由静止释放两带异种电荷的小球,对两小球组成的系统来说,没有外力对它们做功,但它们的动能却增加了,原因也在于它们的内力对它们做了功。
3.动能、动能的变化与动能定理的比较: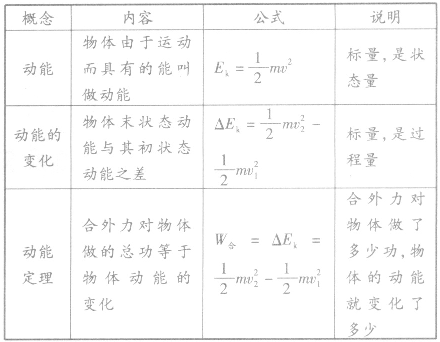
能量守恒定律:
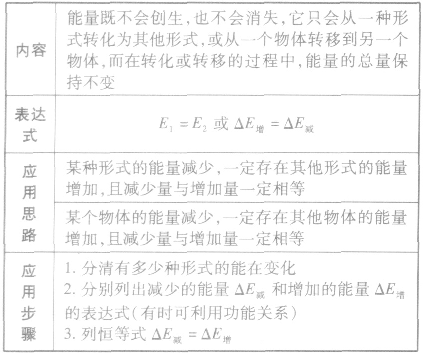
能量守恒中连接体问题的解法:
在两个或两个以上的物体组成的系统中,单独研究其中一个物体时,机械能往往是不守恒的,但对整体来说,机械能又常常是守恒的,所以在这类问题中通常需取整体作为研究对象,再找出其他运动联系来解题。
在判断系统的机械能是否守恒时,除重力、弹力外无其他外力做功,只是系统机械能守恒的必要条件,还需要看系统内力做功的情况。
(1)系统内两个直接接触的物体,如果满足动量守恒和机械能守恒条件,利用两守恒定律是解这类问题的常用方法两物体的运动联系是沿垂直于接触面的分速度相等。
(2)以轻绳相连的两个物体,如果和外界不存在摩擦力做功等问题时,只有机械能在两个物体之间的相互转移,两物体系统机械能守恒。解此类问题的关键是在绳的方向上两物体速度大小相等。
(3)与轻杆相连的物体在绕固定转动轴转动时,两物体的角速度相等。无转动轴时两物体沿杆方向的分速度相等。有摩擦阻力参与过程的能量问题的解法在有摩擦力或介质阻力参与的过程中,机械能不停地向内能转化,但在摩擦力或介质阻力大小不变的情况下,损失的机械能与通过的路程成正比。而在往返运动形式中,通过同一位置时的速率也就不相同,通过同样距离所用时间也不相同。在比较运动时间时,可以通过比较平均速度的大小进而得到时间关系。
点电荷的场强:
1、大小:点电荷产生的电场,某点场强大小与场源电荷的电荷量成正比,与该点到场源电荷的距离的平方成反比
2、方向:场源电荷是正电荷时,某点场强方向沿该点与场源电荷的连线背离场源电荷,场源电荷是负电荷时则相反,如图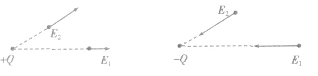
3、表达式:其中Q是场源电荷的电荷量,r是该点到场源电荷的距离
4、适用条件:①真空中②点电荷
1、电势φ:电场中某点的电势等于该点相对零电势点的电势差。
2、特点:
①电势具有相对性,相对参考点而言。但电势之差与参考点的选择无关。通常取离电场无穷远处或大地的电势为零电势。
②电势一个标量,但是它有正负,正负只表示该点电势比参考点电势高,还是低。
③电势的大小由电场本身决定,与Ep和q无关。
④电势在数值上等于单位正电荷由该点移动到零势点时电场力所做的功。
3、电势高低的判断方法
①根据电场线判断:沿着电场线的方向,电势越来越低。
②根据电势能判断:
正电荷:电势能大,电势高;电势能小,电势低。
负电荷:电势能大,电势低;电势能小,电势高。
结论:只在电场力作用下,静止的电荷从电势能高的地方向电势能低的地方运动。
电场的能的性质:
电场力做功的特点在电场中移动电荷时,电场力对电荷做的功只与电荷的起始位置和终止位置有关,而与电荷的运动路径无关。这一点与重力做功的情况类似。沿任一闭合路径移动一周,电场力所做的总功为零。
电势高低的比较方法:
(1)根据电场线或等势面判断。沿电场线方向,电势越来越低,电场线由电势高的等势面指向电势低的等势面。
(2)利用电势差的正负判断。判断出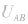 的正负,再由
的正负,再由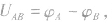 比较
比较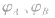 的大小。若
的大小。若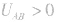 ,则
,则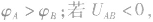 ;则
;则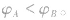
(3)利用场源电荷判断。取无穷远处为零电势点,正电荷周围电势为正值,且离正电荷近处电势高;负电荷周围电势为负值,且离负电荷近处电势低。点电荷电场中某固定点的电势与场源电荷的电性及电荷量有关。场源电荷带正电时,电荷量越大.该点电势越高;场源电荷带负电时则相反。
(4)利用电势叠加判断。苦有多个场源电荷时,每个场源电荷产生的电场中的电势已知或易于判断,可将每个电场的电势先判断后叠加从而得到总电势。
(5)根据电场力做功来判断。正电荷在电场力作用下移动时,电场力做正功,电荷由高电势处移向低电势处;正电荷克服电场力做功,电荷由低电势处移向高电势处。对于负电荷,情况正好相反。
(6)根据电势能判断。正电荷在电势高处电势能较大,负电荷在电势低处电势能较大。
与“如图所示,光滑绝缘的水平面上,相隔2L的A、B两点固定有两个...”考查相似的试题有:
- 质量不等、初动能相等的两物体,在动摩擦因数相同的水平地面上滑行至停止,则( )A.质量大的物体滑行距离长B.质量小的物体...
- 如图所示,一带负电的物体(可当作点电荷)从A点由静止释放,在A点的右方有一带正电的点电荷固定在水平地面上,绝缘物体在电...
- 质量分别为m1、m2的物体放在光滑的水平面上,分别受到不同的恒力F1、F2的作用,由静止开始运动,下列说法正确的是( )A.若...
- 下列说法中正确的是( ) A.一个物体速度方向发生变化,则它的动能一定发生变化. B.两物体质量相同,速度大的物体,其动能...
- 在光滑水平桌面中央固定一边长为0.3m的小正三棱柱abc,俯视如图。长度为L=1m的细线,一端固定在a点,另一端拴住一个质量为m=0...
- (9分)如图所示,用同样材料制成的一个轨道,AB段为1/4圆弧,半径为R=2m,水平放置的BC段长度也为R,一小物块质量为m=1Kg,与...
- 一个质量为0.3kg的弹性小球,在光滑水平面上以6m/s的速度垂直撞到墙上,碰撞后小球沿相反方向运动,反弹后的速度大小与碰撞前...
- 建筑工地上的塔吊起吊重物时,在某段时间内运动轨迹如图所示,开始时重物以速度v0沿水平方向x轴运动,钢丝绳的方向始终沿竖直...
- 如右图所示,虚线表示由点电荷-Q形成的电场中的两个等势面,下列说法正确的是( )A.M点的电势比N点的高B.未确定零电势点前...
- 如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf平面与电场平行,bedf...