本试题 “下列四个图象分别描述甲、乙,丙、丁四个物体的位移、速度、加速度和所受的合外力与时间的关系。关于四个物体的运动,下列说法正确的是[ ]A.甲物体做匀加速...” 主要考查您对v-t图像
s-t图像
其他运动图像
从受力确定运动情况
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- v-t图像
- s-t图像
- 其他运动图像
- 从受力确定运动情况
v—t图像:
物体的运动速度与时间的关系可以用图像来描述。以速度V为纵轴、时间T为横轴建立坐标系,再根据相关数据进项描点,用平滑的曲线将连依次连接起来,就建立了速度时间图象,也就是VT图像。
v—t图像的含义:
1、v-t图象描述速度随时间的变化规律;
2、在速度图像中,可以读出物体在任何时刻的速度;
3、在速度图像中,物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值;
4、在速度图像中,物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率;
5、图线与横轴交叉,表示物体运动的速度反向;
6、图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动。
知识点拨:
 图一
图一
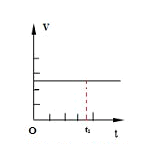
图一是匀速直线运动的v—t的图像,其函数关系式为:v=v,匀速直线运动的物体的速度v是个恒量与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式:S=vt,在图像中为一矩形包围的面积。
 图二
图二
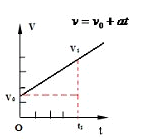
图二是初速度不为0的匀加速直线运动的v—t图像,其函数关系式为: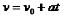 ,匀加速直线运动的物体运动的加速度a(直线的斜率)是个恒量,初速度
,匀加速直线运动的物体运动的加速度a(直线的斜率)是个恒量,初速度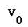 也是恒量,与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式:
也是恒量,与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式: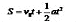 ,在图像中为“矩形+三角形”所包围的面积。
,在图像中为“矩形+三角形”所包围的面积。
v-t图像的基本类型:
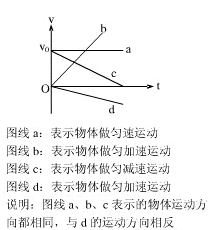
s-t图像:
s-t图像表示运动物体的位置坐标x随时间变化的规律,是运动物体的位置坐标x与时刻t的函数关系图像。位移时间图像是x-t函数图像,而不是物体的运动轨迹。
位移与时间图像的基本意义:
1、s-t图象描述位移随时间的变化规律;
2、图像上一点切线的斜率表示该时刻所对应速度;
3、图像是直线表示物体做匀速直线运动,图像是曲线则表示物体做变速运动;
4、图像与横轴交叉,表示物体从参考点的一边运动到另一边。
知识点拨:
 图一
图一
图一是匀速直线运动的S—t图像,为正比例函数的图像的一部分,其函数关系式为:S=vt,匀速直线运动的物体的速度v(直线的斜率)是个恒量与路程S和时间t没关系。在速度一定的条件下,路程S和时间t成正比。
 图二
图二
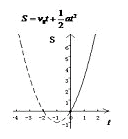
图二是初速度不为0的匀加速直线运动的S—v图像,匀加速直线运动的物体运动的加速度a是个恒量,初速度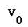 也是恒量,与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式:
也是恒量,与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式: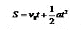 。
。
位移—时间图象(s-t图像):

横轴表示时间,纵轴表示位移;静止的s-t图像在一条与横轴平行或重合的直线上(如右图1①);匀速直线运动的s-t图像在一条倾斜直线上,所在直线的斜率表示运动速度的大小及符号(如右图1②);匀变速直线运动的s-t图像为抛物线(如右图1③)。
1、从图象识别物体的运动性质;
2、能认识图象的截距(即图象与纵轴或横轴的交点坐标)的意义;
3、能认识图象的斜率(即图象与横轴夹角的正切值)的意义;
4、能认识图象与坐标轴所围面积的物理意义;
5、能说明图象上任一点的物理意义。
其他运动图像的例子:
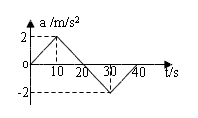 一物体由静止开始沿直线运动,其0~40s的加速度随时间变化。
一物体由静止开始沿直线运动,其0~40s的加速度随时间变化。
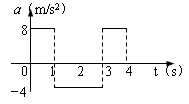 某一物体从静止开始做直线运动,其加速度随时间变化的图像。
某一物体从静止开始做直线运动,其加速度随时间变化的图像。
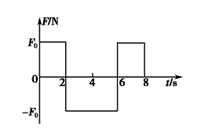 某物体由静止开始做直线运动,物体所受合力F随时间t的变化的图象。
某物体由静止开始做直线运动,物体所受合力F随时间t的变化的图象。
从受力确定运动情况:
1、知道物体受到的全部作用力,应用牛顿第二定律求加速度,再应用运动学公式求出物体的运动情况。
2、分析这两点问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、由物体的受力情况求解物体的运动情况的一般方法和步骤:
①确定研究对象,对研究对象进行受力分析,并画出物体的受力图;
②根据力的合成与分解的方法,求出物体所受的合外力(包括大小和方向);
③根据牛顿第二定律列方程,求出物体的加速度;
④结合给定的物体运动的初始条件,选择运动学公式,求出所需的运动参量,并分析讨论结果是否正确合理。
动力学中临界、极值问题的解决方法:
(1)在运用牛顿运动定律解决动力学有关问题时,常常会讨论相互作用的物体是否会发生相对滑动,相互接触的物体是否会发生分离等,这类问题就是临界问题。临界问题是指物体的运动性质发生突变,要发生而尚未发生改变时的状态。此时运动物体的特殊条件往往是解题的突破口。本部分中常出现的临界条件为:
①绳子或杆的弹力为零;
②相对静止的物体间静摩擦力达到最大,通常在计算中取最大静摩擦力等于滑动摩擦力;
③接触面间弹力为零,但接触物体的速度、加速度仍相等。临界状态往往是极值出现的时刻,题目中常出现隐含临界状态的词语,如“最大”“最小”“最短”“恰好”等.
(2)解决临界问题的关键是要分析出临界状态,例如两物体刚好要发生相对滑动时,接触面上必出现最大静摩擦力,两个物体要发生分离时,相互之间的作用力——弹力必定为零。
(3)解决临界问题的一般方法
①极限法:题设中若出现“最大”“最小…‘刚好”等这类词语时,一般就隐含着临界问题,解决这类问题时,常常是把物理问题(或物理过程)引向极端,进而使临界条件或临界点暴露出来,达到快速解决有关问题的目的。
②假设法:有些物理问题在变化过程中可能会出现临界问题,也可能不出现临界问题,解答这类问题,一般要用假设法。
③数学推理法:根据分析的物理过程列出相应的数学表达式,然后由数学表达式讨论出临界条件。
变加速运动过程的分析方法:
力可以改变速度的大小,也可以改变速度的方向。在牛顿运动定律的应用中,常常会出现物体在变力作用下,对物体的运动情况作出定性判断。处理此类问题的关键是抓住力或加速度与速度之间的方向关系,即同向加速,反向减速,而至于加速度变大或变小,只是影响速度改变的快慢,如在分析自由下落的小球,下落一段时间与弹簧接触后的运动情况时,从它开始接触弹簧到弹簧被压缩到最短的过程中,加速度和速度的变化情况讨论如下(过程图示如图).
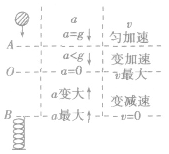
①小球接触弹簧上端后受两个力作用:向下的重力和向上的弹力,在接触后的前一阶段,重力大于弹力,合力向下,因为弹力F=kx不断增大,所以合力不断变小,故加速度也不断减小,由于加速度与速度同向,因此速度不断变大。
②当弹力逐渐增大到与重力大小相等时,合外力为零,加速度为零,速度达到最大。(注意:此位置是两个阶段的转折点)
③后一阶段,即小球到达上述平衡位置之后,由于惯性仍继续向下运动,但弹力大于重力,合力向上,且逐渐变大,因而加速度逐渐变大,方向向上,小球做减速运动,因此速度逐渐减小到零,到达最低点时,弹簧的压缩量最大。
与“下列四个图象分别描述甲、乙,丙、丁四个物体的位移、速度、...”考查相似的试题有:
- 将地面上静止的货物用吊车竖直向上吊起,货物由地面运动到最高点的过程中,货物运动的v一t图象如图 所示,重力加速度g=10m/s2...
- 滑雪者从山上M处以水平速度飞出,经t0时间落在山坡上N处时速度方向刚好沿斜坡向下,接着从N沿直线自由滑下,又经t0时间到达坡...
- 如图所示,是A、B两物体同时由同一地点向同一方向做直线运动的v-t图象,则B物体运动的加速度为___________m/s2,经__________...
- 下图是作直线运动物体的速度-时间图像,其中表示物体作匀变速直线运动的是图( ).
- 竖直升空的火箭,其速度—时间图象如图所示,由图可知以下说法正确的是A.火箭在40s时速度方向发生变化B.火箭上升的最大高度...
- 某质点的图象如图所示,则下列说法中正确的是A.第1s末质点离出发点最远B.第2s末质点运动方向改变C.第3s内和第4s内质点的加...
- 某物体运动的速度图象如图,根据图象可知:( )A.0~2 s内的加速度为1m/s2B.0~5 s内的位移为10mC.第1s末与第3s末速度方...
- (10分)一辆汽车在十字路口等候绿灯,当绿灯亮时,汽车以的加速度开始行驶,恰在此时一辆自行车以的速度匀速驶来,从后面赶...
- 下列图像表示物体做匀速直线运动的是
- 如图所示,质量M = 1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m=1kg,大...