本试题 “在真空中两个带等量异种的点电荷,电量均为2×10-8C,相距20cm,则它们之间的相互作用力为___________N。在两者连线的中点处,电场强度大小为____________N/C...” 主要考查您对库仑定律
电场强度的叠加
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 库仑定律
- 电场强度的叠加
库仑定律:


“割补”法处理非点电荷间的静电力问题:
在应用库仑定律解题时,由于其适用条件是点电荷,所以造成了一些非点电荷问题的求解困难,对于环形或球形缺口问题,“割补法”非常有效。所谓“割”是指将带电体微元化,再利用对称性将带电体各部分所受电场力进行矢量合成。所谓“补”是将缺口部分先补上,使带电体能作为点电荷来处理。
静电力作用的平衡与运动类问题的解法:
带电体在静电力参与下的运动,从运动轨迹来看可以有直线运动、曲线运动;从运动性质来看可以是匀变速运动,也可以是变加速运动;从参与运动的研究对象来看可以是单一的物体,也可以是多物体组成的系统等。物体或者系统在静电力作用下处于平衡状态或某种形式的运动时,解决思路与力学中同类问题的解决思路相同,仍需选定研究对象后进行受力分析,再利用平衡条件或牛顿运动定律列方程求解。但需注意库仑力的特点,特别是在动态平衡问题、运动问题中,带电体间距离发生变化时,库仑力也要发生变化,要分析力与运动的相互影响。整体法与隔离法是解决连接体问题的有效方法,在通过静电力联系在一起的系统,也要注意考虑整体法与隔离法的选择。
知识拓展:
三个点电荷在相互间作用力作用下处于平衡时的规律
规律一:三个点电荷的位置关系是“同性在两边,异性在中间”:如果三个点电荷只在库仑力的作用下能够处于平衡状态,则这三个点电荷一定处于同一直线上,且有两个是同性电荷,一个是异性电荷,两个同性电荷分别在异性电荷的两边。
规律二:中间的电荷所带电荷量是三个点电荷中电荷量最小的;两边同性电荷谁的电荷量小,中间异性电荷就距谁近一些.
证明:如图所示,甲、乙、丙三个点电荷处于平衡状态,它们的电荷量分别为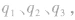 甲与乙、乙与丙之间的距离分别为
甲与乙、乙与丙之间的距离分别为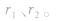 设
设 为正电荷,则
为正电荷,则 为负电荷。由公式F=qE知,三个电荷能够处于平衡状态,说明甲、乙、丙三个电荷所在处的合场强为0。
为负电荷。由公式F=qE知,三个电荷能够处于平衡状态,说明甲、乙、丙三个电荷所在处的合场强为0。
乙、丙两点电荷在甲处产生的场强分别为
 两场强在甲处大小相等,方向相反,合场强等于零,故
两场强在甲处大小相等,方向相反,合场强等于零,故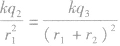 ,由此式可知
,由此式可知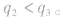 同理可证
同理可证
规律三:三个点电荷的电荷量满足
证明:三个点电荷能够同时处于平衡状态,则三个点电荷之间的库仑力相等,即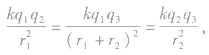
整理该式易得 ,
,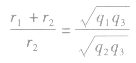
联立两式得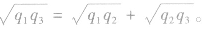
三个自由电荷都处于平衡状态时,则口诀概括为 “三点共线,两同夹异(同性在两边,异性在中间),两大夹小,近小远大,高考不怕”。由此可以迅速、准确地确定三个电荷的相对位置及电性。
场强的叠加:
当空间有几个带电体同时存在时,它们的电场就互相叠加,形成合电场,这时某点的场强就等于各个带电体单独存在时在该点产生场强的矢最和。
如果各个带电体的场强已知,则可用求矢量和的方法求出合场强,常用的方法有平行四边形法、正交分解法、图解法等。
匀强电场中确定电势及场强方向的“等分法” :
已知匀强电场中几点的电势,如果要求其他点的电势或场强的方向时,一般可利用“等分法”。即在电势差相差最大的两点的连线上,将某一线段等分时,每一小段线段两端电势差相等,从而找到与已知或待求点电势相等的等势点。连接等势点可得等势线,作等势线的垂线可确定电场线,结合电势升降可得电场强度的方向。
“拆分法”处理不等量点电荷电场中的问题:
两个不等量点电荷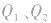 形成的电场。设
形成的电场。设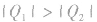 ,则可将
,则可将 拆分为
拆分为 两个点电荷,其中一部分与
两个点电荷,其中一部分与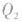 形成了等量点电荷的电场,则整个电场可看成两等量点电荷
形成了等量点电荷的电场,则整个电场可看成两等量点电荷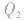 与点电荷
与点电荷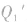 所产生的电场的叠加。
所产生的电场的叠加。
与“在真空中两个带等量异种的点电荷,电量均为2×10-8C,相距20cm...”考查相似的试题有:
- 如图所示,在粗糙水平面上,彼此靠近地放置两个带同种电荷的小物块.由静止释放后,两个物块向相反方向运动,并最终停止.在...
- 真空中两个带电量均为q的点电荷间距离为r时,它们之间的库仑力大小为F;若保持它们间距离不变,将其中一个点电荷变为2q,它们...
- 如图所示,两根细线拴着两个质量相同的小球A、B,上、下两根细线中的拉力分别是TA、TB,现在使A、B带同种电荷,此时上、下细...
- 宇航员在探测某星球时有如下发现:(1)该星球带负电,而且带电均匀;(2)该星球表面没有大气;(3)在一次实验中,宇航员将...
- 宇航员在探测某星球时有如下发现:(1)该星球带负电,而且带电均匀;(2)该星球表面没有大气;(3)在一次实验中,宇航员将一个带...
- 在真空中,两个很小的带电体相距为d时,相互的排斥力为F.保持它们的带电量不变,要使斥力变为16F,这时两个带电体之间的距离...
- 真空中有两个固定点电荷q1与q2,若电荷量都变为原来的2倍,则它们间的库仑力变为原来的( )A.14倍B.12倍C.2倍D.4倍
- 如图把一带正电的小球a放在光滑绝缘斜面上,欲使球a能静止在斜面上,需在MN间放一带电小球b,则应放[ ]A、带负电,放在A点B、...
- 两带电量分别为q和-q的点电荷放在x轴上,相距为L,能正确反映两电荷连线上场强大小E与x关系的是图( ) A. B. C. D.
- 如图所示,A、B为带电量分别是Q和-Q的两个等量异种点电荷,A、B间的距离为r,则AB中点处O点的场强大小为______N/C,方向向___...