本试题 “一列沿x轴正方向传播的简谐波,其波源位于坐标原点O,且在t=0时刻的波形图如图所示.已知这列波在P出现两次波峰的最短时间是0.4 s,求:(1)这列波的波速;(2...” 主要考查您对简谐运动的表达式
机械波的形成和传播
波长、频率和波速
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 简谐运动的表达式
- 机械波的形成和传播
- 波长、频率和波速
简谐运动:
1.定义:如果质点的位移与时间的关系遵从正弦函数的规律,即它的振动图像(x一t图像)是一条正弦曲线,这样的振动叫做简谐运动
2.位移表达式:![]() 。其中x为位移,A为振幅,ω为角频率,φ为相位。
。其中x为位移,A为振幅,ω为角频率,φ为相位。
3.特征:
(1)动力学特征: F=-kx
回复力大小与位移大小成正比,方向与位移方向相反
(2)运动学特征: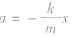
简谐运动的判定方法:
(1)简谐运动的位移一时间图像是正弦曲线或余弦曲线。
(2)做简谐运动的物体所受力满足F=-kx,即回复力符合F和x成正比且方向总相反。
用F=-kx判定振动是否是简谐运动的步骤:
①对振动物体进行受力分析;
②沿振动方向对力进行合成与分解;
③找出回复力,判断是否符合F=-kx。
机械运动:
1、定义:机械振动在介质中传播的过程。
2、机械波产生的条件:①振源;②介质。
3、波的形式:由于介质中质点间存在着相互作用力,波源的振动就带动周围质点的振动,周围质点的振动再带动其邻近质点的振动,于是振动就在介质中由近及远地传播出去,形成了波
4、机械波的特点:
①机械波传播的是振动形式和能量。质点只在各自的平衡位置附近振动,并不随波迁移;
②介质中各质点的振动周期和频率都与波源的振动周期和频率相同;
③离波源近的质点带动离波源远的质点依次振动。
5、波动与振动的关系:
波动中一定有振动,振动不一定形成波。波动是大量质点的振动,振动是单一质点的振动
振动是波动形成的原因,波动是振动传播的结果
波长:
1.定义:在波动中,振动相位总是相同的两个相邻质点间的距离,叫做波长,通常用λ表示
另一种定义方式:两个相邻的、在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长
2.意义:波长反映了波在空间的周期性
平衡位置相距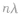 的质点振动相同,平衡位置相距
的质点振动相同,平衡位置相距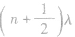 的质点振动相反(其中n=0,l,2…)
的质点振动相反(其中n=0,l,2…)
3.备注:①注意定义中两个要素:“总是”,“相邻”
②在横波中两个相邻的波峰(或波谷)间的距离等于波长。在纵波中两个相邻的密部(或疏部)间的距离等于波长。
③在一个周期内机械波传播的距离等于一个波长
周期与频率:
1.概念:在波动中,各个质点的振动周期或频率是相同的,它们都等于波源的振动周期或频率,这个周期或频率也叫做波的周期或频率
2.关系:频率与周期的关系:
3.备注:①波源振动一个周期,被波源带动的质点刚好完成一个全振动,波在介质中传播一个波长
②波的频率等于单位时间内波形成完整波的个数;等于单位时间内通过介质中某点完整波形的个数;等于介质内已开始振动的任一质点在单位时间内完成全振动的次数;等于单位时间内沿波传播方向上传播距离与波长的比值,即传播距离内包含完整波形的个数
③每经历一个周期,波形图重复一次
波速:
1.定义:单位时间内振动向外传播的距离
2.定义式:
3.意义:波速是指振动在介质中传播的快慢程度
4.备注:波速与质点振动速度不同,且与其无关
三者关系:
1.定量关系:经过一个周期T,振动在介质中传播的距离等于一个波长λ,所以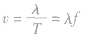
2.决定因素:(1)周期T和频率f取决于波源,与v、λ无关,与介质无关。波从一种介质进人另一种介质时,周期和频率是不变的。
(2)波速v由介质本身性质决定,与f,λ无关。
(3)波长λ决定于v和f(或T),只要v和f其中一个改变,λ就改变
质点振动方向与波的传播方向的互判方法:
已知质点的振动方向可判断波的传播方向;相反,已知波的传播方向可判断质点的振动方向。
1.上下坡法
沿波的传播方向看,“上坡”的点向下振动,“下坡”的点向上振动,简称“上坡下,下坡上”。如图所示。
逆着波的传播方向看,“上坡”的点向上振动,“下坡’’的点向下振动。 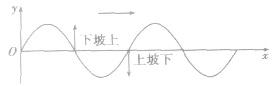
2.同侧法
在波的图像上的某一点,沿纵轴方向画出一个箭头表示质点振动方向,并设想在同一点沿x轴方向画一个箭头表示波的传播方向,那么这两个箭头总是在曲线的同侧。如图所示。 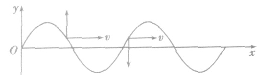
3.带动法(特殊点法)
如图所示为一沿x轴正方向传播的横波,根据波的形成,靠近波源的点能带动它邻近的离波源稍远的点,可判断质点的振动方向。在质点P附近靠近波源一方的图线上另找一点P',若P’在P上方,P '带动P向上运动,则P向上运动;若P’在P下方,P带动 P’向下运动,则P’向下运动。 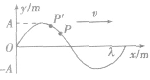
4.微平移法
将波形沿波的传播方向做微小移动,如图中虚线所示,由于质点仅在y轴方向上振动,所以,
 即质点运动后的位置,故该时刻A、B沿y轴正方向运动,C、D沿y轴负方向运动。
即质点运动后的位置,故该时刻A、B沿y轴正方向运动,C、D沿y轴负方向运动。
与“一列沿x轴正方向传播的简谐波,其波源位于坐标原点O,且在t=...”考查相似的试题有:
- 一列横波沿x轴正方向传播,t0=0时刻的波形如图所示,此时波刚好传到x=3 m处,此后x=1 m处的质点比x=-l m处的质点____(填“先”...
- 机械波在传播的过程中,正确的说法是( )A.介质中的质点是随波迁移的B.波源的振动能量是由近及远地传播C.机械波的传播需...
- 如图所示,为一列横波沿着一条右端固定的绳子从A点传播到B点的波形示意图,由图可判断出A开始振动的方向是( )A.向左B.向...
- 一简谐机械波沿x轴正方向传播,波长为λ,周期为T.图1为该波在t=T2时刻的波形图,a、b是波上的两个质点.图2表示介质中某一质...
- 如图是一列简谐横波的图象,由图可知,其振幅为______,波长为______.
- 如图所示是一列向右传播的横波,波速为0.4m/s,M点的横坐标x=10m,图示时刻波传到N点.现从图示时刻开始计时,经过______s时...
- 波源S1和S2振动方向相同,频率均为4 Hz,分别置于均匀介质中x轴上的O、A两点处,OA=2 m,如图所示。两波源产生的简谐横波沿x...
- A、B两船每分钟上下振动20次,水波的波速为2m/s,当A位于平衡位置时,B位于波谷,A、B两船之间还有5个波谷,则两船间的水平距...
- 一列横波在t时刻的波形如图所示,振幅为1 cm,已知质点M开始振动的时间比质点N迟0.1 s,两质点的平衡位置相距2 cm,此时刻质...
- 如图所示是一列横波上A、B两质点的振动图象,该波由A传向B,两质点沿波的传播方向上的距离Δx=4.0m,波长大于3.0m,求这列波的...