密度公式的应用：
（1）利用m=ρV求质量；利用V=m/ρ求体积

（2）对于密度公式，还要从以下四个方面理解
①同种物质，在一定状态下密度是定值，它不随质量大小或体积大小的改变而改变。当其质量（或体积）增大几倍时，其体积（或质量）也随着增大几倍，而比值是不变的。因此，不能认为物质的密度与质量成正比，与体积成反比；
②具有同种物质的物体，在同一状态下，体积大的质量也大，物体的体积跟它的质量成正比；
③具有不同物质的物体，在体积相同的情况下，密度大的质量也大，物体的质量跟它的密度成正比；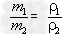

④具有不同物质的物体，在质量相同的条件下，密度大的体积反而小，物体的体积跟它的密度成反比。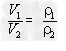

密度公式的应用：
1. 有关密度的图像问题
此问题一般是给出质量一体积图像，判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值，然后在纵坐标(或横坐标)上找到对应的数值，进行分析比较。
 例1如图所示，是甲、乙两种物质的m一V图像，由图像可知(   )
A．ρ_甲>ρ_乙
B．ρ_甲=ρ_乙
C．ρ_甲<ρ_乙
D．无法确定甲、乙密度的大小

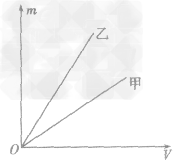
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到，我们要先借助图像，根据公式ρ =总结规律后方可。
如图所示，在横轴上任取一点V₀，由V₀作横轴的垂线V₀B，分别交甲、乙两图线于A、B两点，再分别从A、B两点作纵轴垂线，分别交纵轴于m_甲、m_乙两点。则甲、乙两种物质的密度分别为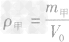，ρ_乙= 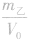，因为m_甲<m_乙，所以ρ甲<ρ乙，故C正确。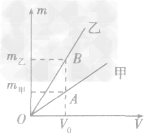

2. 密度公式ρ =及变形、m=ρV的应用：
密度的公式是ρ =，可得出质量计算式m=ρV 和体积计算式。只要知道其中两个物理量，就可以代入相应的计算式进行计算。审题时注意什么量是不变的，什么量是变化的。
例2某瓶氧气的密度是5kg/m³，给人供氧用去了氧气质量的一半，则瓶内剩余氧气的密度是_____；容积是10L的瓶子装满了煤油，已知煤油的密度是 0．8×10³kg/m³，则瓶内煤油的质量是_____，将煤油倒去4kg后，瓶内剩余煤油的密度是______。
 解析：氧气用去一半，剩余部分仍然充满整个氧气瓶，即质量减半体积不变，所以氧气的密度变为 2．5kg/m³。煤油倒去一半后，体积质量同时减半，密度不变。
答案：2．5kg/m³；8kg；0．8×10kg/m³。

3. 比例法求解物质的密度
   利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是：题目所描述的物理现象，由初始状态到终结状态的过程中至少有一个量保持不变，这个不变的量是由初始状态变成终结状态的桥梁，我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3：2，体积之比为l：3，那么它们的密度之比为(   )
A．1：2B．2：1C．2：9D．9：2
解析：（1）写出所求物理量的表达式：，
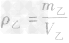
（2）写出该物理量比的表达式：

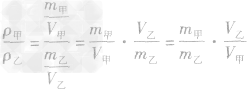
（3）化简：代入已知比值的求解：


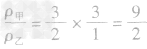
密度、质量、体积计算中的“隐含条件” 问题：
  很多物理问题中的有些条件需要仔细审题才能确定，这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例，密度计算题形式多样，变化灵活，但其中有一些题具有这样的特点：即质量、体积、密度中的某个量在其他量发生变化时保持不变，抓住这一特点，就掌握了求解这类题的规律。

1．隐含体积不变
例1一个瓶子最多能装0．5kg的水，它最多能装_____kg的水银，最多能装_____m³的酒精。 ρ水银=13．6×10³kg／m³，ρ水=1．0×10³kg／m³，ρ酒精= 0．8×10³kg／m³)
解析:最多能装即装满瓶子，由最多装水量可求得瓶子的容积为V=5×10^-4m³，则装水银为m_水银=13．6×10³kg／m³×5×10^-4m³=6．8kg。装酒精的体积为瓶子的容积。
答案6．8；5×10^-4

2. 隐含密度不变
例2一块石碑的体积为V_样=30m³，为测石碑的质量，先取了一块刻制石碑时剔下来的小石块作为样品，其质量是m_样=140g，将它放入V₁=100cm³的水中后水面升高，总体积增大到V₂=150cm³，求这块石碑的质量m_碑。
解析：此题中隐含的条件是石碑和样品是同种物质，密度相同，而不同的是它们的体积和质量。依题意可知，样品体积为：
V_样=V₂-V₁=150cm³一100cm³=50cm³ =5．0×10^-5m³
得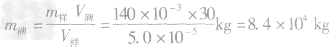=84t
答案：84t

3. 隐含质量不变
例3质量为450g的水结成冰后，其体积变化了 ____m3。(ρ水=0．9×10³kg／m³)
解析：水结成冰后，密度减小，450g水的体积为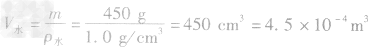，水结成冰后，质量不变，因此冰的体积为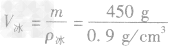=500cm³=5．0×10^-4m³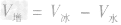，=5．0× 10^-4m³一4．5×10^-4m³=5×10^-5m³。

合金物体密度的相关计算：
     首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征，然后根据具体问题，灵活求解。
例两种不同的金属，密度分别为ρ1、ρ2：
(1)若墩质量相等的金属混合后制成合金，则合金的密度为____。
(2)若取体积相等的金属混合后制成合金，则合金的密度为_____。
解析：这道题的关键是抓住“两总”不变，即总质量和总体积不变。在(1)中，两种金属的质量相等，设为m1=m2=m，合金的质量m_总=2m，则密度为ρ1的金属的体积V1=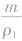，密度为ρ2的金属的体积V2=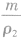，合金的体积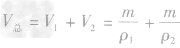，则合金的密度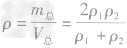
在（2）中两种金属的体积相等，设为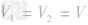，合金的体积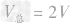，密度为ρ1的金属的质量m1=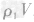，密度为ρ2的金属的质量为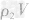，合金的质量m总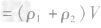，合金的密度为。
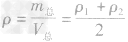答案：
注意：上述规律也适用于两种液体的混合，只要混合液的总质量和总体积不变即可。

核能和获得核能的途径：
核外电子：带负电
1．原子结构
2．核能：质子、中子依靠强大的核力紧密地结合存一起，一旦使原子分裂或聚合，就可能释放出惊人的能量，这就是核能。
3．目前获得核能有两条途径：核裂变、核聚变。

核裂变：
1．核裂变：把重核分裂成质量较小的核，释放出核能的反应称为核裂变。
2．核裂变的原理——链式反应：原子核持续裂变，并释放出大量的核能。如图：
 
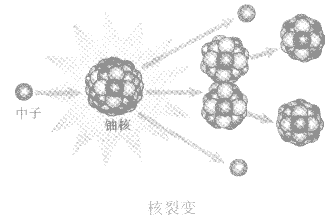
3．应用：原子弹、核电站的能量都来源于核裂变，下图为我国第一颗原子弹爆炸图。


核聚变（热核反应）
1．核聚变是产生核能的另一种方式。核聚变是较轻的原子核结合成为较重的原子核的一种反应。
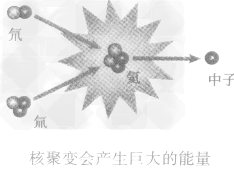
2．如图所永的是氘核和氚核结合成为氦核的聚变过程。这种核反应也伴随着释放巨大的能量。
3．利用核聚变反应也能制造核武器。氢弹就是利用核聚变原理制造的一种威力比原子弹还要大的核武器(如图)。

4．核聚变需要超高温度，因此核聚变也被称作热核反应。在太阳中，发生的就是热核反应。

核电站及核反应堆：
1．构成核反应堆是产生核反应的装置，是核电站的核心。核反应堆一般由铀棒(核材料)、减速剂、控制棒、冷却剂、热交换器和屏蔽物(水泥)等组成(如图)。


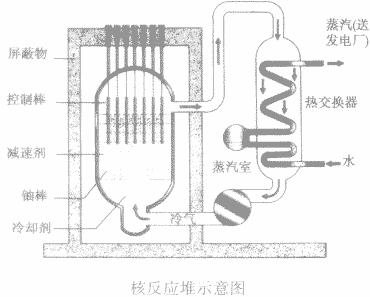
2．原理它的基本工作原理是这样的：核材料在反应堆内部发生核反应产生热量；用石墨或其他材料制成的减速剂使核反应产生的中子减速以提高核裂变的效率；控制棒的下部为阻挡中子的材料，用来控制链式反应的速度，如果希望加快反应速度就把控制棒拉出来一点，希望降低反应速度则推进控制棒；冷却剂在反应堆中循环以将热量带入热交换器；水在热交换器中被加热成为蒸汽以输出用于推动汽轮机，再带动发电机发电。

3．能量转化过程核能→水和水蒸气的内能→蒸汽轮机的机械能→电能。

4．提示原子弹和核反应堆巾发生的都是核裂变，它们的区别是：原子弹爆炸时发生的链式反应是不加控制的；而通过核反应堆，可将链式反应的速度加以控制，使其平稳地释放出大量核能。