返回

高中三年级数学

首页
首页 高中三年级数学知识 曲线的方程 椭圆的性质（顶点、范围、对称性、离心率） 试题正文
  • 解答题
    已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由。


    本题信息：2003年高考真题数学解答题难度极难 来源:张玲玲
  • 本题答案
    查看答案
本试题 “已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE与OF的交点（如图），问是否存在两个定点，使P到这两点...” 主要考查您对

曲线的方程

椭圆的性质（顶点、范围、对称性、离心率）

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 曲线的方程
  • 椭圆的性质（顶点、范围、对称性、离心率）

曲线的方程的定义：

在直角坐标系中，如果某曲线C（看作点的集合或适合某种条件的点的轨迹）上的点与一个二元方程f（x，y）=0的实数解建立了如下的关系：
（1）曲线上点的坐标都是这个方程的解；
（2）以这个方程的解为坐标的点都是曲线上的点。
那么，这个方程叫做曲线的方程，这条曲线叫做方程的曲线。

求曲线的方程的步骤：

（1）建立适当的坐标系，用有序实数对（x，y）表示曲线上任意一点M的坐标；
（2）写出适合条件的p（M）的集合，P={M|p（M）}；
（3）用坐标表示条件p（M），列出方程f（x，y）=0；
（4）化方程f（x，y）=0为最简形式；
（5）说明化简后的方程的解为坐标的点都在曲线上。


求曲线的方程的步骤：

（1）建立适当的坐标系，用有序实数对（x，y）表示曲线上任意一点M的坐标；
（2）写出适合条件的p（M）的集合，P={M|p（M）}；
（3）用坐标表示条件p（M），列出方程f（x，y）=0；
（4）化方程f（x，y）=0为最简形式；
（5）说明化简后的方程的解为坐标的点都在曲线上。

求曲线方程的常用方法：

（1）待定系数法这种方法需要预先知道曲线的方程，先设出来，然后根据条件列出方程（组）求解未知数。
（2）直译法就是把动点所满足的题设条件直接给表示出来，从而得到其横、纵坐标之间的关系式。（3）定义法就是由曲线的定义直接得到曲线方程。
（4）交轨法：就是在求两动曲线交点轨迹方程时，联立方程组消去参数，得到交点的轨迹方程。在求交点问题时常用此法。
（5）参数法就是通过中间变量找到y、x的间接关系，然后通过消参得出其直接关系。
（6）相关点法就是通过所求动点与已知动点的关系，来求曲线方程的方法。


 椭圆的离心率：

椭圆的焦距与长轴长之比叫做椭圆的离心率。


椭圆的性质：

1、顶点：A（a，0），B（-a，0），C（0，b）和D（0，-b）。
2、轴：对称轴：x轴，y轴；长轴长|AB|=2a，短轴长|CD|=2b，a为长半轴长，b为短半轴长。
3、焦点：F1（-c，0），F2（c，0）。
4、焦距：。
5、离心率：；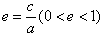 
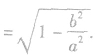
离心率对椭圆形状的影响：e越接近1，c就越接近a，从而b就越小，椭圆就越扁；e越接近0，c就越接近0，从而b就越大，椭圆就越圆；
6、椭圆的范围和对称性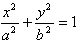：（a＞b＞0）中-a≤x≤a，-b≤y≤b，对称中心是原点，对称轴是坐标轴。
。


利用椭圆的几何性质解题：

利用椭圆的几何性质可以求离心率及椭圆的标准方程．要熟练掌握将椭圆中的某些线段长用a，b，c表示出来，例如焦点与各顶点所连线段的长，过焦点与长轴垂直的弦长等，这将有利于提高解题能力。

椭圆中求最值的方法：

求最值有两种方法：
(1)利用函数最值的探求方法利用函数最值的探求方法，将其转化为函数的最值问题来处理．此时应充分注意椭圆中x，y的范围，常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义，寻找图形中的几何元素、几何量之间的关系．

椭圆中离心率的求法：

在求离心率时关键是从题目条件中找到关于a，b，c的两个方程或从题目中得到的图形中找到a，b，c的关系式，从而求离心率或离心率的取值范围．


发现相似题
与“已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O为AB的中点，点E...”考查相似的试题有：