本试题 “细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为530,如图所示,以下说法正确的是(已知cos530=...” 主要考查您对共点力的平衡
从受力确定运动情况
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 共点力的平衡
- 从受力确定运动情况
共点力:
作用在物体的同一点,或作用线相交于一点的几个力。
平衡状态:
物体保持匀速直线运动或静止叫平衡状态,是加速度等于零的状态。
共点力作用下的物体的平衡条件:
物体所受的合外力为零,即∑F=0,若采用正交分解法求解平衡问题,则平衡条件应为:∑Fx=0,∑Fy=0。
解决平衡问题的常用方法:
隔离法、整体法、图解法、三角形相似法、正交分解法等。
图解法分析分力与合力的关系:
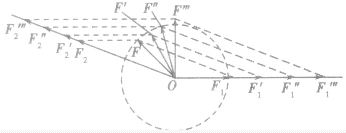
当两个分力成一定的夹角α(α<180。)时,增大其中一个分力或使两个分力都增大,合力的变化情况如何呢?这个问题可以用数学公式推导分析,也可以用函数图像数形结合分析,但最简捷有效的方法是图解法。为了便于分析合力的变化,设 ,借助辅助参考圆来进行分析。如图所示,F1、F2的共点在圆心,而且开始时F1、F2的合力为F,大小恰好为圆的半径。
,借助辅助参考圆来进行分析。如图所示,F1、F2的共点在圆心,而且开始时F1、F2的合力为F,大小恰好为圆的半径。
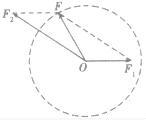
(1)当保持力F2不变,只增大F1时,如图所示,合力,的大小可能出现三种情况:减小、不变或增大,即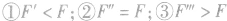 。我们可以得到这样的结论:当两个力F1、F1夹角α保持不变,在增大其中一个分力时,它们的合力大小可能减小、不变或增大。
。我们可以得到这样的结论:当两个力F1、F1夹角α保持不变,在增大其中一个分力时,它们的合力大小可能减小、不变或增大。
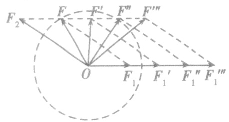
(2)当两个分力F1、F2都增大时,如图所示,合力F 的大小也有可能出现三种情况:减小、不变或增大,即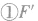
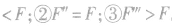 ,我们也可以得到这样的结论:当两个力F1、F2夹角α保持不变,在同时增大两个分力时,它们的合力F大小可能减小、不变或增大。
,我们也可以得到这样的结论:当两个力F1、F2夹角α保持不变,在同时增大两个分力时,它们的合力F大小可能减小、不变或增大。
整体法与隔离法:
(1)整体法:当只涉及研究系统而不涉及系统内部某些物体的力和运动时,一般可采用整体法。运用整体法解题的基本步骤是:
①明确研究的系统和运动的全过程;
②画出系统整体的受力图和运动全过程的示意图;
③选用适当的物理规律列方程求解。
(2)隔离法:为了弄清系统(连接体)内某个物体的受力和运动情况,一般可采用隔离法。运用隔离法解题的基本步骤是:
①明确研究对象或过程、状态;
②将某个研究对象或某段运动过程、某个状态从全过程中隔离出来;
③画出某状态下的受力图或运动过程示意图;
④选用适当的物理规律列方程求解。隔离法和整体法常常需交叉运用,从而优化解题思路和方法,使解题简捷明了。
受力分析的一般顺序:
(1)明确研究对象,研究对象可以是质点、结点、物体、物体系。
(2)找出所有接触点。
(3)按顺序分析物体受力。一般先分析场力(重力、电场力、磁场力等不接触力).再依次对每一接触点分析弹力、摩擦力。
(4)找出每个力的施力物体。(防“多”分析力)
(5)看受力与运动状态是否相符。(防“漏”力、 “错”力)
(6)正确画出受力图。注意不同对象的受力图用隔离法分别画出,对于质点和不考虑力对物体的形变和转动效果的情况,可将各力平移至物体的重心上,即各力均从重心画起。
受力分析的步骤:
第一步:隔离物体。隔离物体就是把被分析的那个物体或系统单独画出来,而不要管其周围的其他物体,这是受力分析的基础。
第二步:在已隔离的物体上画出重力和其他已知力。重力是一个已知力,可首先把它画出来。另外,物体往往在重力及其他主动力作用下才与其他物体产生挤压、拉伸以及相对运动等,进而产生弹力和摩擦力,所以还要分析其他主动力。第三步:查找接触点和接触面。就是查找被分析物体与其他物体的接触点和接触面。弹力和摩擦力是接触力,其他物体对被分析物体的弹力和摩擦力只能通过接触点和接触面来作用,这就是说寻找物体所受的弹力(拉力、压力、支持力等)和摩擦力只能在被分析物体与其他物体相接触的点和面上找。查找接触点和接触面要全,每个接触点或面上最多有两个力(一个弹力,一个摩擦力)。
第四步:分析弹力(拉力、压力、支持力等)。在被分析物体与其他物体的接触处,如果有形变(挤压或拉伸),则该处就有弹力,反之则没有。在确定弹力存在以后,其方向就比较容易确定了。
第五步:分析摩擦力。摩擦力分静摩擦力和滑动摩擦力,它们的产生条件是两物体接触处不光滑,除挤压外还要有相对滑动的趋势或相对滑动。因此分析接触面上有无摩擦力,首先要看接触面是否光滑(这是题目中的已知条件),其次看有无弹力,然后再进行摩擦力的判断:接触面上有相对滑动时有滑动摩擦力,其大小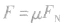 ,方向跟物体的相对运动方向相反;接触面上无相对滑动但有相对滑动趋势时有静摩擦力,它的大小和方向总是跟迫使物体产生相对滑动趋势的外力有关。
,方向跟物体的相对运动方向相反;接触面上无相对滑动但有相对滑动趋势时有静摩擦力,它的大小和方向总是跟迫使物体产生相对滑动趋势的外力有关。
受力分析中的技巧:
(1)研究对象的受力图,通常只画出根据性质命名的力,不要把按效果分解的分力或合力分析进去,受力图完成后再进行力的合成或分解。
(2)区分内力和外力。对几个物体的整体进行受力分析时,这几个物体间的作用力为内力,不能在受力图中出现;当把某一物体单独隔离分析时,原来的内力变成了外力,要画在受力图上。
(3)在难以确定物体的某些受力情况时,可先根据 (或确定)物体的运动状态,再运用平衡条件或牛顿运动定律来判定未知力。也就是说在分析物体受力时要时刻结合研究对象所处的运动状态,同时对不易确定的力。可结合牛顿第三定律来分析其反作用力是否存在以及方向如何等情况。
作用在物体的同一点,或作用线相交于一点的几个力。
平衡状态:
物体保持匀速直线运动或静止叫平衡状态,是加速度等于零的状态。
共点力作用下的物体的平衡条件:
物体所受的合外力为零,即∑F=0,若采用正交分解法求解平衡问题,则平衡条件应为:∑Fx=0,∑Fy=0。
解决平衡问题的常用方法:
隔离法、整体法、图解法、三角形相似法、正交分解法等。
图解法分析分力与合力的关系:
当两个分力成一定的夹角α(α<180。)时,增大其中一个分力或使两个分力都增大,合力的变化情况如何呢?这个问题可以用数学公式推导分析,也可以用函数图像数形结合分析,但最简捷有效的方法是图解法。为了便于分析合力的变化,设
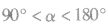 ,借助辅助参考圆来进行分析。如图所示,F1、F2的共点在圆心,而且开始时F1、F2的合力为F,大小恰好为圆的半径。
,借助辅助参考圆来进行分析。如图所示,F1、F2的共点在圆心,而且开始时F1、F2的合力为F,大小恰好为圆的半径。
(1)当保持力F2不变,只增大F1时,如图所示,合力,的大小可能出现三种情况:减小、不变或增大,即
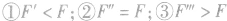 。我们可以得到这样的结论:当两个力F1、F1夹角α保持不变,在增大其中一个分力时,它们的合力大小可能减小、不变或增大。
。我们可以得到这样的结论:当两个力F1、F1夹角α保持不变,在增大其中一个分力时,它们的合力大小可能减小、不变或增大。
(2)当两个分力F1、F2都增大时,如图所示,合力F 的大小也有可能出现三种情况:减小、不变或增大,即
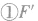
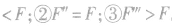 ,我们也可以得到这样的结论:当两个力F1、F2夹角α保持不变,在同时增大两个分力时,它们的合力F大小可能减小、不变或增大。
,我们也可以得到这样的结论:当两个力F1、F2夹角α保持不变,在同时增大两个分力时,它们的合力F大小可能减小、不变或增大。
整体法与隔离法:
(1)整体法:当只涉及研究系统而不涉及系统内部某些物体的力和运动时,一般可采用整体法。运用整体法解题的基本步骤是:
①明确研究的系统和运动的全过程;
②画出系统整体的受力图和运动全过程的示意图;
③选用适当的物理规律列方程求解。
(2)隔离法:为了弄清系统(连接体)内某个物体的受力和运动情况,一般可采用隔离法。运用隔离法解题的基本步骤是:
①明确研究对象或过程、状态;
②将某个研究对象或某段运动过程、某个状态从全过程中隔离出来;
③画出某状态下的受力图或运动过程示意图;
④选用适当的物理规律列方程求解。隔离法和整体法常常需交叉运用,从而优化解题思路和方法,使解题简捷明了。
受力分析的一般顺序:
(1)明确研究对象,研究对象可以是质点、结点、物体、物体系。
(2)找出所有接触点。
(3)按顺序分析物体受力。一般先分析场力(重力、电场力、磁场力等不接触力).再依次对每一接触点分析弹力、摩擦力。
(4)找出每个力的施力物体。(防“多”分析力)
(5)看受力与运动状态是否相符。(防“漏”力、 “错”力)
(6)正确画出受力图。注意不同对象的受力图用隔离法分别画出,对于质点和不考虑力对物体的形变和转动效果的情况,可将各力平移至物体的重心上,即各力均从重心画起。
受力分析的步骤:
第一步:隔离物体。隔离物体就是把被分析的那个物体或系统单独画出来,而不要管其周围的其他物体,这是受力分析的基础。
第二步:在已隔离的物体上画出重力和其他已知力。重力是一个已知力,可首先把它画出来。另外,物体往往在重力及其他主动力作用下才与其他物体产生挤压、拉伸以及相对运动等,进而产生弹力和摩擦力,所以还要分析其他主动力。第三步:查找接触点和接触面。就是查找被分析物体与其他物体的接触点和接触面。弹力和摩擦力是接触力,其他物体对被分析物体的弹力和摩擦力只能通过接触点和接触面来作用,这就是说寻找物体所受的弹力(拉力、压力、支持力等)和摩擦力只能在被分析物体与其他物体相接触的点和面上找。查找接触点和接触面要全,每个接触点或面上最多有两个力(一个弹力,一个摩擦力)。
第四步:分析弹力(拉力、压力、支持力等)。在被分析物体与其他物体的接触处,如果有形变(挤压或拉伸),则该处就有弹力,反之则没有。在确定弹力存在以后,其方向就比较容易确定了。
第五步:分析摩擦力。摩擦力分静摩擦力和滑动摩擦力,它们的产生条件是两物体接触处不光滑,除挤压外还要有相对滑动的趋势或相对滑动。因此分析接触面上有无摩擦力,首先要看接触面是否光滑(这是题目中的已知条件),其次看有无弹力,然后再进行摩擦力的判断:接触面上有相对滑动时有滑动摩擦力,其大小
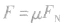 ,方向跟物体的相对运动方向相反;接触面上无相对滑动但有相对滑动趋势时有静摩擦力,它的大小和方向总是跟迫使物体产生相对滑动趋势的外力有关。
,方向跟物体的相对运动方向相反;接触面上无相对滑动但有相对滑动趋势时有静摩擦力,它的大小和方向总是跟迫使物体产生相对滑动趋势的外力有关。受力分析中的技巧:
(1)研究对象的受力图,通常只画出根据性质命名的力,不要把按效果分解的分力或合力分析进去,受力图完成后再进行力的合成或分解。
(2)区分内力和外力。对几个物体的整体进行受力分析时,这几个物体间的作用力为内力,不能在受力图中出现;当把某一物体单独隔离分析时,原来的内力变成了外力,要画在受力图上。
(3)在难以确定物体的某些受力情况时,可先根据 (或确定)物体的运动状态,再运用平衡条件或牛顿运动定律来判定未知力。也就是说在分析物体受力时要时刻结合研究对象所处的运动状态,同时对不易确定的力。可结合牛顿第三定律来分析其反作用力是否存在以及方向如何等情况。
从受力确定运动情况:
1、知道物体受到的全部作用力,应用牛顿第二定律求加速度,再应用运动学公式求出物体的运动情况。
2、分析这两点问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、由物体的受力情况求解物体的运动情况的一般方法和步骤:
①确定研究对象,对研究对象进行受力分析,并画出物体的受力图;
②根据力的合成与分解的方法,求出物体所受的合外力(包括大小和方向);
③根据牛顿第二定律列方程,求出物体的加速度;
④结合给定的物体运动的初始条件,选择运动学公式,求出所需的运动参量,并分析讨论结果是否正确合理。
动力学中临界、极值问题的解决方法:
(1)在运用牛顿运动定律解决动力学有关问题时,常常会讨论相互作用的物体是否会发生相对滑动,相互接触的物体是否会发生分离等,这类问题就是临界问题。临界问题是指物体的运动性质发生突变,要发生而尚未发生改变时的状态。此时运动物体的特殊条件往往是解题的突破口。本部分中常出现的临界条件为:
①绳子或杆的弹力为零;
②相对静止的物体间静摩擦力达到最大,通常在计算中取最大静摩擦力等于滑动摩擦力;
③接触面间弹力为零,但接触物体的速度、加速度仍相等。临界状态往往是极值出现的时刻,题目中常出现隐含临界状态的词语,如“最大”“最小”“最短”“恰好”等.
(2)解决临界问题的关键是要分析出临界状态,例如两物体刚好要发生相对滑动时,接触面上必出现最大静摩擦力,两个物体要发生分离时,相互之间的作用力——弹力必定为零。
(3)解决临界问题的一般方法
①极限法:题设中若出现“最大”“最小…‘刚好”等这类词语时,一般就隐含着临界问题,解决这类问题时,常常是把物理问题(或物理过程)引向极端,进而使临界条件或临界点暴露出来,达到快速解决有关问题的目的。
②假设法:有些物理问题在变化过程中可能会出现临界问题,也可能不出现临界问题,解答这类问题,一般要用假设法。
③数学推理法:根据分析的物理过程列出相应的数学表达式,然后由数学表达式讨论出临界条件。
变加速运动过程的分析方法:
力可以改变速度的大小,也可以改变速度的方向。在牛顿运动定律的应用中,常常会出现物体在变力作用下,对物体的运动情况作出定性判断。处理此类问题的关键是抓住力或加速度与速度之间的方向关系,即同向加速,反向减速,而至于加速度变大或变小,只是影响速度改变的快慢,如在分析自由下落的小球,下落一段时间与弹簧接触后的运动情况时,从它开始接触弹簧到弹簧被压缩到最短的过程中,加速度和速度的变化情况讨论如下(过程图示如图).
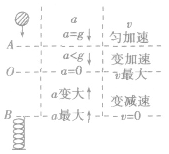
①小球接触弹簧上端后受两个力作用:向下的重力和向上的弹力,在接触后的前一阶段,重力大于弹力,合力向下,因为弹力F=kx不断增大,所以合力不断变小,故加速度也不断减小,由于加速度与速度同向,因此速度不断变大。
②当弹力逐渐增大到与重力大小相等时,合外力为零,加速度为零,速度达到最大。(注意:此位置是两个阶段的转折点)
③后一阶段,即小球到达上述平衡位置之后,由于惯性仍继续向下运动,但弹力大于重力,合力向上,且逐渐变大,因而加速度逐渐变大,方向向上,小球做减速运动,因此速度逐渐减小到零,到达最低点时,弹簧的压缩量最大。
发现相似题
与“细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,...”考查相似的试题有:
- 如图所示,在水平面上的箱子内,带异种电荷的小球a、b用绝缘细线分别系于箱子上、下两边并处于静止状态,此时地面受到的压力...
- 2012年伦敦奥运会,我国运动员陈一冰勇夺吊环亚军,其中有一个高难度的动作就是先双手撑住吊环(设开始时两绳与肩同宽),然...
- 分别对下列A、B图中小球、C图中杆、D图中B物体作受力分析,并画出受力示意图。(A中小球用细绳挂在光滑的墙上,B中小球用细绳...
- 如图所示,在倾角都为θ的光滑导轨上,放一根长为l、质量为m的金属棒ab,在通电金属棒所在空间存在磁感应强度为B、方向竖直向...
- (19分)某兴趣小组用如图甲所示装置进行研究,现有N个这样的装置:用长为l=2R的轻绳系着半径为R的光滑小球,小球的质量为m....
- 如图所示,长为L的轻质细杆OA,O端为转轴,固定于竖直墙壁上,A端绕接(固定)两条细绳,一绳栓重力为G的重物,另一绳跨过墙...
- 运动员双手紧握竹竿匀速攀升和匀速下滑时,所受的摩擦力分别是f1和f2,则( )A.f1向下,f2向上,且f1=f2B.f1向下,f2向上...
- 如图所示,图乙中用力F取代图甲中的m,且F=mg,其余器材完全相同,不计摩擦,图甲中小车的加速度为a1,图乙中小车的加速度为...
- 如图甲所示,放在光滑水平面上的木块受到两个水平力F1与F2的作用,静止不动,现保持力F1不变,使力F2逐渐减小到零,再逐渐恢...
- 雨滴从高空由静止下落,由于空气阻力作用,其加速度逐渐减小,直到为零,在此过程中雨滴的运动情况是[ ]A.速度一直保持不变B...