本试题 “如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h。物块B质量是小球的5倍,置于粗糙的水平面上且位于O点正下方,物块与水平面间的...” 主要考查您对机械能守恒定律
动量定理
碰撞
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 机械能守恒定律
- 动量定理
- 碰撞
1、内容:只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变。
2、表达式:
3.条件
机械能守恒的条件是:只有重力或弹力做功。可以从以下三个方面理解:
(1)只受重力作用,例如在不考虑空气阻力的情况下的各种抛体运动,物体的机械能守恒。
(2)受其他力,但其他力不做功,只有重力或弹力做功。例如物体沿光滑的曲面下滑,受重力、曲面的支持力的作用,但曲面的支持力不做功,物体的机械能守恒。
(3)其他力做功,但做功的代数和为零。
判定机械能守恒的方法:
(1)条件分析法:应用系统机械能守恒的条件进行分析。分析物体或系统的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力 (或弹力)做功,没有其他力做功或其他力做功的代数和为零,则系统的机械能守恒。
(2)能量转化分析法:从能量转化的角度进行分析:若只有系统内物体间动能和重力势能及弹性势能的相互转化,系统跟外界没有发生机械能的传递,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒。
(3)增减情况分析法:直接从机械能的各种形式的能量的增减情况进行分析。若系统的动能与势能均增加或均减少,则系统的机械能不守恒;若系统的动能不变,而势能发生了变化,或系统的势能不变,而动能发生了变化,则系统的机械能不守恒;若系统内各个物体的机械能均增加或均减少,则系统的机械能不守恒。
(4)对一些绳子突然绷紧、物体间非弹性碰撞等,除非题目特别说明,否则机械能必定不守恒。
竖直平面内圆周运动与机械能守恒问题的解法:
在自然界中,违背能量守恒的过程肯定是不能够发生的,而不违背能量守恒的过程也不一定能够发生,因为一个过程的进行要受到多种因素的制约,能量守恒只是这个过程发生的一个必要条件。如在竖直平面内的变速圆周运动模型中,无支撑物的情况下,物体要到达圆周的最高点,从能量角度来看,要求物体在最低点动能不小于最高点与最低点的重力势能差值。但只满足此条件物体并不一定能沿圆弧轨道运动到圆弧最高点。因为在沿圆弧轨道运动时还需满足动力学条件:所需向心力不小于重力,由此可以推知,在物体从圆弧轨道最低点开始运动时,若在动能全部转化为重力势能时所能上升的高度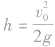 满足
满足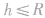 时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在
时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在 ,物体上升到圆周最高点时的速度
,物体上升到圆周最高点时的速度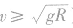 )时,物体可做完整的圆周运动;若在
)时,物体可做完整的圆周运动;若在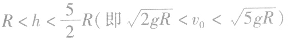 时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度
时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度 满足
满足 。故在解决这类问题时不能单从能量守恒的角度来考虑。
。故在解决这类问题时不能单从能量守恒的角度来考虑。
1、内容:物体所受合外力的冲量等于它的动量的变化。
2、表达式:Ft=p'-p或Ft=mv'-mv。
3、注意:
①动量定理公式是一矢量式,运用它分析问题时要特别注意冲量、动量及动量变化量的方向;
②公式中的F是研究对象所受的包括重力在内的所有外力的合力;
③动量定理的研究对象可以是单个物体,也可以是物体系统。对物体系统,只需分析系统受的外力,不必考虑系统内力;系统内力的作用不改变整个系统的总动量;
④动量定理不仅适用于恒定的力,也适用于随时间变化的力。对于变力,动量定理中的力F应当理解为变力在作用时间内的平均值。
冲量,动量与动量变化:
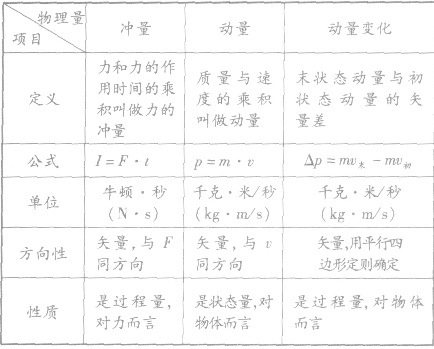
动量变化:
(1)动量变化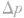 的表达式:
的表达式: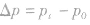 。(此式为矢量式)。
。(此式为矢量式)。
(2)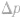 的求法:
的求法:
①若 在同一直线上,则先规定正方向,再用正负表示
在同一直线上,则先规定正方向,再用正负表示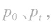 然后进行代数运算求解。
然后进行代数运算求解。
②若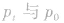 不在同一直线上,则用平行四边形定则(或三角形定则)求矢量差。
不在同一直线上,则用平行四边形定则(或三角形定则)求矢量差。
(3)△p的方向:△p的方向与速度的变化量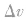 的方向相同。
的方向相同。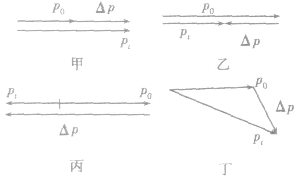
动量和能量的综合问题的解法:
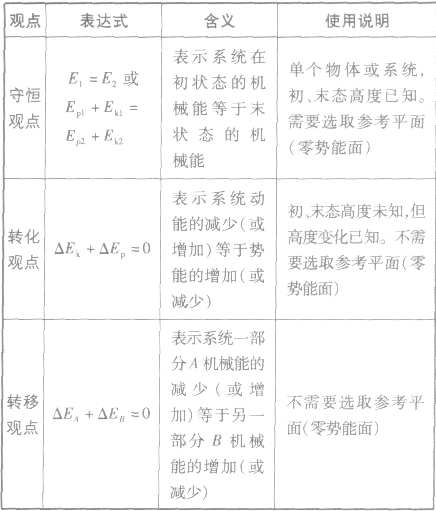
1.动量的观点与能量的观点
(1)动量的观点:动量定理和动量守恒定律。
(2)能量的观点:动能定理和能量守恒定律。这两个观点研究的是物体或系统运动变化所经历的过程中状态的改变,它无需对过程是怎样变化的细节进行深入的研究,而关心的是运动状态变化即改变的结果量及其引起变化的原因,简单地说,只要知道过程的始末状态动量式、动能式和力在过程中的冲量和所做的功,即可对问题求解。
2.利用动量观点和能量观点解题时应注意的问题动量定理和动量守恒定律是矢量表达式,还可写出分量表达式,而动能定理和能量守恒定律是标量表达式,绝无分量表达式。
1、特点:
①时间:过程持续时间即相互作用时间极短
②作用力:在相互作用的过程中,相互作用力先是急剧增大,然后再急剧减小,平均作用力很大
③动量守恒条件:系统的内力远远大于外力,所以,系统即使所受外力之和不为零,外力也可以忽略,系统的总动量守恒
④位移:碰撞过程是在一瞬间发生的,时间极短,所以,在物体发生碰撞的瞬间,可忽略物体的位移,可以认为物体在碰撞前后仍在同一位置
⑤能量:在碰撞过程中,一般伴随着机械能的损失,碰撞后系统的总动能要小于或等于碰撞前系统的总动能,
2、两物体相碰通常有以下三种情况
①两物体碰撞后,动能无损失,称为弹性碰撞。当两相等质量的物体发生弹性碰撞时,则发生速度交换,这是一个很有用的结论。
②两物体碰撞后虽分开,但动能有损失,称为非弹性碰撞。
③两物体碰撞后合为一个整体,以某一共同速度运动,称为完全非弹性碰撞。此类碰撞中动能损失最多,即动能转化为其他形式能的值最多。
弹性碰撞及讨论:
质量为m1与质量为m2的物体分别以速度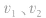 运动并发生对心碰撞,碰撞过程中无机械能损失(如图所示)。
运动并发生对心碰撞,碰撞过程中无机械能损失(如图所示)。
设碰后两物体的速度分别为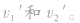
据动量守恒得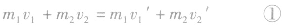
据机械能守恒得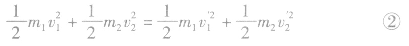
由①②两式得
由上述表达式可以看出:
(1)若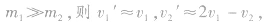
(2)若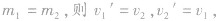 即速度交换。
即速度交换。
(3)若 ,即m2的速度几乎不变。
,即m2的速度几乎不变。
“一动一静”模型:
(1)弹性正碰,如图所示,在光滑水平面上质量为 m1的小球以速度v1与质量为m2的静止小球发生弹性正碰.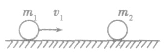
讨论碰后两球的速度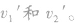 根据动量守恒和机械能守恒有:
根据动量守恒和机械能守恒有: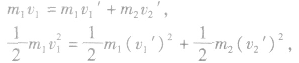
解上面两式可得:
碰后m1的速度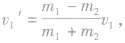
碰后m2的速度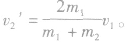
讨论:
①若表示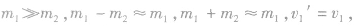
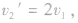 表示m1的速度不变,m2以2v1速度被撞出去。
表示m1的速度不变,m2以2v1速度被撞出去。
②若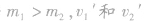 都是正值,表示
都是正值,表示 都与v1方向相同。
都与v1方向相同。
③若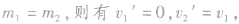 ,则有即碰后两球速度互换。
,则有即碰后两球速度互换。
④若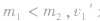 为负值,表示
为负值,表示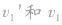 方向相反, m1被弹回。
方向相反, m1被弹回。
⑤若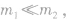 这时
这时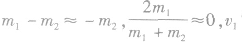
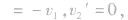 表示m1被反向以原速率弹回,而m2仍静止。
表示m1被反向以原速率弹回,而m2仍静止。
⑥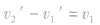
两物体碰后的速度随两物体的质量比变化情况如图所示。 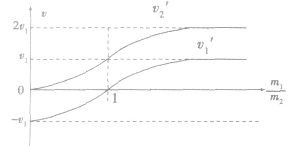
⑦能量传递:在弹性碰撞中,传递的能量跟两者质量比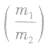 有关,即
有关,即
 两球质量越接近,碰撞中传递的动能越大;在
两球质量越接近,碰撞中传递的动能越大;在 两种情况下,传递的动能相等。
两种情况下,传递的动能相等。
(2)完全非弹性碰撞上例中m1与m2发生完全非弹性碰撞,则有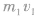
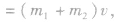 ,碰后的共同速度
,碰后的共同速度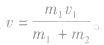
损失的动能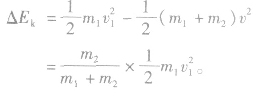
“二合一”模型:
这种模型是指两个速度不同的物体通过发生相互作用,最终两物体粘在一起运动或以共同的速度运动的模型。
这种模型的主要特征是终态共速(也可以是只在某一时刻共速.而研究的过程是从初始到共速的过程),从能量角度来看,这种过程中能量损失是最大的,属于完全非弹性碰撞的类型,在一维碰撞中的方程有: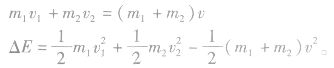
相互作用的两个物体在很多情况下皆可当成碰撞处理,那么对相互作用中两物体相距“恰最近”、相距 “恰最远”或“恰上升到最高点”等一类,临界问题,求解的关键都是“速度相等”。在“类碰撞”问题中,碰撞时间不一定很短,但遵守的规律却是相同的,例如下面几种情形。
(1)如图中,光滑水平面上的A物体以速度v0去撞击静止的B物体,A、B两物体相距最近时,两物体速度必定相等,此时弹簧最短,其压缩量最大,系统损失的动能等于弹簧获得的弹性势能, 
(2)在图中,物体A以速度v0滑到静止在光滑水平面上的小车B上,当A在B上滑行的距离最远时,A、B相对静止,A、B的速度必定相等,系统损失的动能等于AB间摩擦产生的热量。 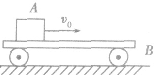
(3)在图中,子弹以速度v0射入静止在光滑的水平面上的木块中。当子弹不穿出时,子弹和木块的速度必定相等,系统损失的动能等于子弹与木块间摩擦产生的热量。 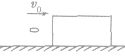
(4)如图所示,质量为M的滑块静止在光滑水平面上,滑块的光滑弧面底部与桌面相切,一个质量为m 的小球以速度v0向滑块滚来。设小球不能越过滑块,则小球到达滑块上的最高点时(即小球在竖直方向上的速度为零),两者的速度肯定相等(方向为水平向右),小球获得的重力势能等于系统损失的动能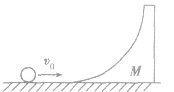
碰撞合理性的判断方法:
碰撞的合理性要遵循动量守恒定律、能量关系和速度关系:
1.系统动量守恒
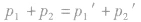
2.碰撞过程中系统的总动能不会增加
如果物体发生的是弹性碰撞,总动能不变;其他情况碰撞后会有部分动能转化为内能,系统的动能将减小。即 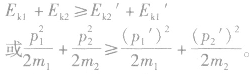
3.速度要符合情景如果碰前两物体同向运动,则后面物体的速度必大于前面物体的速度,即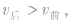 否则无法实现碰撞。碰撞后,原来在前的物体速度一定增大,且原来在前的物体速度大于或等于原来在后的物体速度,即
否则无法实现碰撞。碰撞后,原来在前的物体速度一定增大,且原来在前的物体速度大于或等于原来在后的物体速度,即
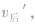 否则碰撞没有结束。如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零。
否则碰撞没有结束。如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零。
与“如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到...”考查相似的试题有:
- 如图所示,一根轻绳上端固定在O点、下端拴一个重为G的钢球 A,O点到球心距离为l,开始时球悬垂静止.现对球施加一个方向始终...
- 如图所示,倾角为θ=30°的足够长的固定斜面上,在底端0处固定一垂直斜面的档板,斜面上OM段光滑,M点及以上均粗糙.质量为m的...
- 质量分别为m和3m的物块A、B用一根轻弹簧连接,置于光滑的水平面上,物块A刚好与墙接触。先用外力缓慢向左推物块B使弹簧压缩,...
- 如图所示,弹簧下面挂一质量为m的物体,物体在竖直方向上作振幅为A的简谐运动,当物体振动到最高点时,弹簧正好为原长,弹簧...
- 小明和小强在操场上一起踢足球,足球质量为m。如图所示,小明将足球以速度v从地面上的A点踢起,当足球到达离地面高度为h的B点...
- 如图所示,光滑平面上,两个相隔一定距离的小球分别以v0和0.8v0的速度反向匀速运动,它们中间另有两个小球(小球1和小球2)将...
- 2010年1月4日,828米高的全球最高楼--哈里发大楼(此前称为“迪拜塔”)举行了落成启用典礼,如图所示.风速曾是修建的关键,一...
- 一瀑布落差为h=20m,水流量为Q=0.10m3/s,水的密度ρ=1.0×103kg/m3,水在最高点和落至石头上后的速度都认为是零,试估算水对石...
- 如图所示,质量为m的小球在竖直光滑圆形内轨道中做圆周运动,周期为T,则①每运转一周,小球所受重力的冲量的大小为0②每运转一...
- 某消防队员从一平台上跳下,下落2米后双脚触地,接着他用双腿弯曲的方法缓冲,使自身重心又下降了0.5米,在着地过程中地面对...