本试题 “在开展研究性学习的过程中,某同学设计了一个利用线圈测量转轮转动角速度的装置.如图所示,在轮子的边缘贴上小磁体,将小线圈靠近轮边放置,接上数据采集器...” 主要考查您对线速度
角速度
法拉第电磁感应定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 线速度
- 角速度
- 法拉第电磁感应定律
线速度的定义:
质点沿圆周运动通过的弧长与所用时间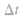 的比值叫做线速度。
的比值叫做线速度。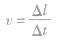 ,
,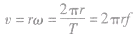 。
。
线速度的特性:
线速度是矢量,方向和半径垂直,和圆周相切。它是描述做圆周运动的物理运动快慢的物理量。
对线速度的理解:
物体上任一点对定轴作圆周运动时的速度称为“线速度”。它的一般定义是质点作曲线运动时所具有的顺时速度。它的方向沿运动轨道的切线方向,故又称切向速度。它是描述作曲线运动的质点运动快慢和方向的物理量。物体上各点作曲线运动时所具有的顺时速度,其方向沿运动轨道的切线方向。 (高中物理中的切线方向就指速度一侧的方向,和数学中的切线不同)
知识点拨:
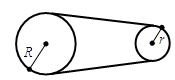
如图,大圆和小圆有同一根皮带相连,皮带上的各个点的速率相同,所以大圆和小圆圆周上的线速度是相同的。
角速度的定义:
圆周运动中,连接质点和圆心的半径转过的角度 跟所用时间
跟所用时间 的比值叫做角速度。
的比值叫做角速度。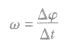 ,
,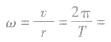
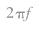 。
。
角速度的特性:
角速度是矢量,高中阶段不研究其方向。它是描述做圆周运动的物体绕圆心转动快慢的物理量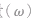 。
。
单位:在国际单位制中,单位是“弧度/秒”(rad/s)。(1rad=360d°/(2π)≈57°17'45″)
转动周数时(例如:每分钟转动周数),则以转速来描述转动速度快慢。角速度的方向垂直于转动平面,可通过右手螺旋定则来确定。(角速度的方向,在高中物理的学习不属于考察的内容)
线速度和角速度的对比:
角速度是单位时间转过的角度;或者说是转过的角度和所用时间的比值。
线速度是单位时间走过的弧长;或者说是弧长和所用时间的比值。
角速度和线速度的关系:
知识拓展提升:
例:计算地球和月亮公转的角速度:

通过计算知道,书中所提到的地球和月球的争论是没有结论的。比较运动得快慢,要看比较线速度还是角速度,不能简单说谁快谁慢。
法拉第电磁感应定律:
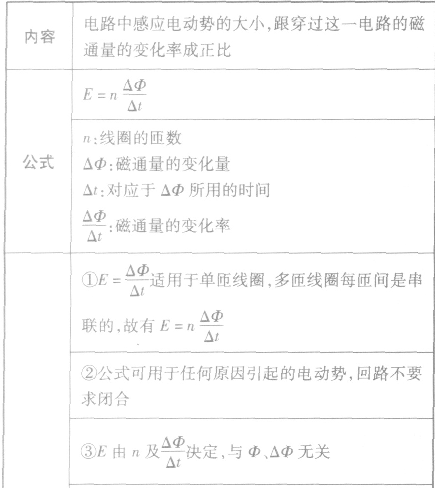

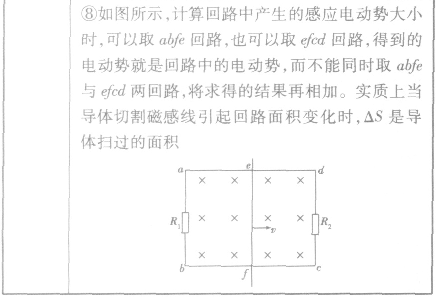
导体切割磁感线的两个特例:

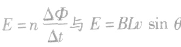 的区别与联系及选用原则:
的区别与联系及选用原则: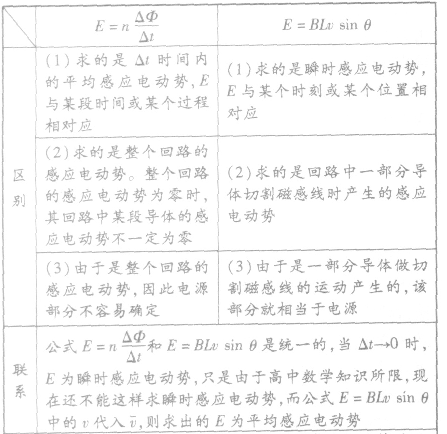

电磁感应中动力学问题的解法:
电磁感应和力学问题的综合,其联系的桥梁是磁场对感应电流的安培力,因为感应电流与导体运动的加速度有相互制约的关系。
1.分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力,用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2.常见的动态分析这类问题中的导体一般不是做匀变速运动,而是经历一个动态变化过程再趋于一个稳定状态,故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析,研究顺序为:导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环,循环结束时,加速度等于零.导体达到稳定运动状态。
电磁感应中的动力学临界问题:
(1)解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度求最大值或最小值的条件。
(2)基本思路: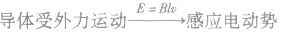
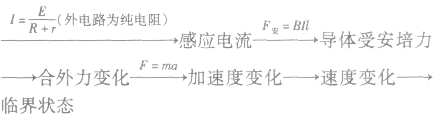
与“在开展研究性学习的过程中,某同学设计了一个利用线圈测量转...”考查相似的试题有:
- 如图所示是自行车传动装置的示意图,若脚蹬匀速转一圈需要时间T,已数出链轮齿数为48,飞轮齿数为16,要知道在此情况下自行车...
- 不同的物理量可以有相同的单位.下列各组物理量中有相同单位的是( )A.速度和角速度B.电压和电动势C.电势和电势能D.磁通...
- 如图所示,半径足够大的圆盘M水平放置,绕过其圆心的竖直轴OO′匀速转动,规定经过O点且水平向右为x轴正方向.在圆心O点正上方...
- 如图所示的皮带传动装置中,A、B两轮半径分别为rA和rB,已知rA<rB,且皮带不打滑.在传动过程中,下列说法正确的是( )A.A...
- 如图所示,竖直平面内半圆形管道ADB固定在CD杆上,AB为直径,CD过圆心O且与AB垂直,半圆管道右半BD部分光滑,左半AD部分有摩...
- 升降机内悬挂一圆锥摆,摆线长为1m,小球质量为0.5kg,当升降机以2m/s2的加速度匀加速上升时,摆线恰好与竖直方向成θ=37°角,...
- 汽车自动控制刹车系统(ABS)的原理如图所示.铁质齿轮P与车轮同步转动,右端有一个绕有线圈的磁体(极性如图),M是一个电流...
- 如图所示,金属杆ab静放在水平固定的“U”形金属框上,整个装置处于竖直向上的磁场中.当磁感应强度均匀增大时,杆ab总保持静止...
- (11分)如左图所示,两根足够长的光滑直金属导轨、平行放置在倾角为的绝缘斜面上,两导轨间距为。、两点间接有阻值为的电阻...
- 穿过一个电阻为2Ω的闭合线圈的磁通量每秒钟均匀地减少8Wb,则[ ]A. 线圈中感应电动势每秒钟增加8VB. 线圈中感应电流每秒钟减...