本试题 “如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤...” 主要考查您对功
重力势能
能量转化与守恒定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 功
- 重力势能
- 能量转化与守恒定律
功:
1、功的定义:力和作用在力的方向上通过的位移的乘积。是描述力对空间积累效应的物理量,是过程量。
2、功的两个必要因素:作用在物体上的力;物体在力的方向上发生的位移。
3、功的定义式:W=Fscosα,其中F是恒力,s是作用点的位移,α是力与位移间的夹角(功的单位焦耳,简称焦,符号J)。
4、功的计算
①恒力的功可根据W=FScosα进行计算,本公式只适用于恒力做功;
②根据W=P·t,计算一段时间内平均做功;
③利用动能定理计算力的功,特别是变力所做的功;
④根据功是能量转化的量度反过来可求功。
力做功情况的判定方法:
一个力对物体做不做功,是做正功还是做负功,判断的方法是:
(1)看力与位移之间的夹角,或者看力与速度之间的夹角:为锐角时,力对物体做正功;为钝角时,力对物体做负功;为直角时,力对物体不做功。
(2)看物体间是否有能量转化:若有能量转化,则必定有力做功。此方法常用于相连的物体做曲线运动的情况。
变力做功的求法:
公式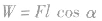 只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
1.用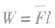 求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用
求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用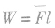 求变力F所做的功。其平均值大小 为
求变力F所做的功。其平均值大小 为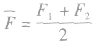 ,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
2.用微元法(或分段法)求变力做功变力做功时,可将整个过程分为几个微小的阶段,使力在每个阶段内不变,求出每个阶段内外力所做的功,然后再求和。当力的大小不变而方向始终与运动方向间的夹角恒定时,变力所做的功形: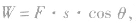 其中s是路程。
其中s是路程。
3.用等效法求变力做功若某一变力做的功等效于某一恒力做的功,则可以应用公式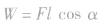 来求。这样,变力做功问题就转化为了恒力做功问题。
来求。这样,变力做功问题就转化为了恒力做功问题。
4.用图像法求变力做功存F—l图像中,图线与两坐标轴所围“面积”的代数和表示F做的功,“面积”有正负,在l轴上方的“面积”为正,在l轴下方的“面积”为负。
5.应用动能定理求变力做功
如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能变化量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
6.利用功能关系求变力做功
在变力做功的过程中,当有重力势能、弹性势能以及其他形式的能量参与转化时,可以考虑用功能关系求解。因为做功的过程就是能量转化的过程,并且转化过程中能量守恒。
7.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是恒定的。若功率P是变化的,则需用 计算,其中当P随时间均匀变化时,
计算,其中当P随时间均匀变化时, 。
。
由物体问相互作用和相对位置决定的能量叫做势能。例如:重力势能、弹性势能、分子势能、电势能等。
重力做功与重力势能的比较:
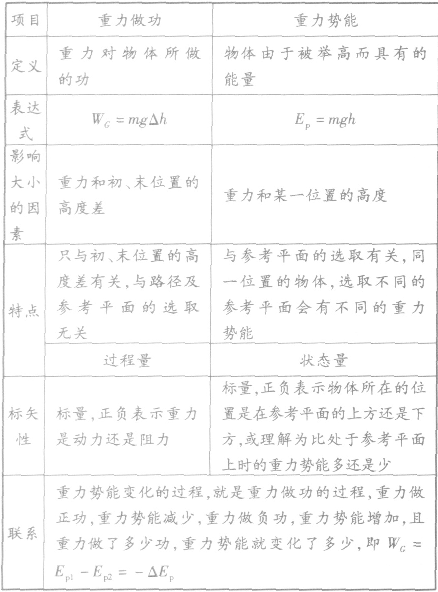
能量守恒定律:
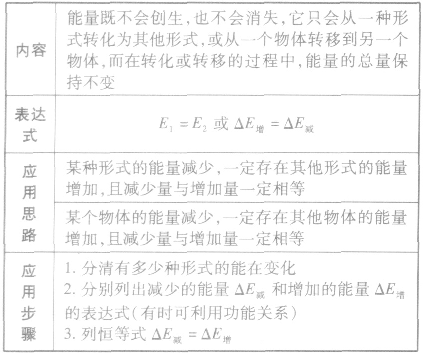
能量守恒中连接体问题的解法:
在两个或两个以上的物体组成的系统中,单独研究其中一个物体时,机械能往往是不守恒的,但对整体来说,机械能又常常是守恒的,所以在这类问题中通常需取整体作为研究对象,再找出其他运动联系来解题。
在判断系统的机械能是否守恒时,除重力、弹力外无其他外力做功,只是系统机械能守恒的必要条件,还需要看系统内力做功的情况。
(1)系统内两个直接接触的物体,如果满足动量守恒和机械能守恒条件,利用两守恒定律是解这类问题的常用方法两物体的运动联系是沿垂直于接触面的分速度相等。
(2)以轻绳相连的两个物体,如果和外界不存在摩擦力做功等问题时,只有机械能在两个物体之间的相互转移,两物体系统机械能守恒。解此类问题的关键是在绳的方向上两物体速度大小相等。
(3)与轻杆相连的物体在绕固定转动轴转动时,两物体的角速度相等。无转动轴时两物体沿杆方向的分速度相等。有摩擦阻力参与过程的能量问题的解法在有摩擦力或介质阻力参与的过程中,机械能不停地向内能转化,但在摩擦力或介质阻力大小不变的情况下,损失的机械能与通过的路程成正比。而在往返运动形式中,通过同一位置时的速率也就不相同,通过同样距离所用时间也不相同。在比较运动时间时,可以通过比较平均速度的大小进而得到时间关系。
与“如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静...”考查相似的试题有:
- 下列说法正确的是( )A.当作用力做正功时,反作用力一定做负功B.当作用力不做功时,反作用力也不做功C.作用力做正功,反...
- 在光滑水平面上,物体受两个相互垂直的大小分别为F1="3" N和F2="4" N 的恒力,其合力在水平方向上,物体从静止开始沿合力方向...
- 如图所示,在皮带传送装置中,皮带把物体P匀速带至低处(物体与皮带相对静止),在此过程中,下述说法正确的( )A.支持力对...
- 游乐场中有一种叫“空中飞椅”的设施,其基本装置是将绳子上端固定在转盘的边缘上,绳子下端连接座椅,人坐在座椅上随转盘旋转...
- 如图所示,木块A放在木块B的左端,用恒力F将木块A 拉到板B的右端。第一次将B固定在地面上,F做功为W1,系统产生的热量为Q1;...
- 关于摩擦力做功,下列叙述正确的是( )A.摩擦力做功的多少只与起始和终了位置有关,与运动路径无关B.滑动摩擦力总是做负功C...
- 如图所示,重球m用一条不可伸长的轻质细线拴住后悬于O点,重球置于一个斜面劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由...
- 一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点...
- 一架波音客机的总质量为2 ×105kg,在它升高2.5km 的过程中,(1)客机克服重力做了多少功?(2)重力势能变化了多少?(取g=10 m/...
- 某型号的“神舟飞船”顺利发射升空后,在离地面340km的圆轨道上运行了108圈。运行中需要多次进行“轨道维持”。所谓“轨道维持”就...