本试题 “物理学中用到大量的科学方法,建立下列概念时均用到“等效替代”方法的是( )A.“合力与分力”、“质点”、“电场强度B.“质点”、“平均速度”、“点电荷”C.“点电荷”...” 主要考查您对质点
平均速度和瞬时速度的区别
力的合成
电荷、元电荷
电场强度的定义式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 质点
- 平均速度和瞬时速度的区别
- 力的合成
- 电荷、元电荷
- 电场强度的定义式
质点的定义:
质点是忽略物体的大小和形状简化成的有质量的点。它是一种科学的抽象,是一个理想化的物理模型,是在研究物体运动时,抓住主要因素,忽略次要因素,对实际物体进行的近似。
质点的特性:
(1)它没有大小和形状
(2)它具有物体的全部质量
(3)它是一种理想化的模型,实际生活中并不存在
可将物体视为质点的三种情况:
(1)运动物体的大小跟它与另一被研究的对象间的距离相比可忽略不计时,可将该物体当做质点。
(2)做平动的物体,由于物体上各个点运动的情况相同,可以选物体上任一点的运动来代表物体的运动,故平动的物体在研究其运动性质时,可将它视为质点。
(3)有转动,但相对平动而言可以忽略时,也可以把物体视为质点。如汽车在运行时,虽然车轮有转动,但我们关心的是车辆整体运动的快慢,故汽车可以看成质点。
对质点的理解:
①质点是为了研究物体的运动而建立的物理模型,是对实际物体科学的抽象,现实中的质点是不存在的.
②物体能否看成质点是由所研究问题的性质决定的.同一物体在有些情况下可以看成质点,而在另一些情况下又不能看成质点.如研究火车过桥的时间时就不能把火车看成质点,但研究火车从北京到上海所用时间时就可把火车看成质点.
例1.关于质点的以下说法正确的是( )
A.只有体积很小或质量很小的物体才可以看成质点
B.只要物体的运动不是很快,物体就可以看成质点
C.物体的大小和形状在所研究的现象中起的作用很小,可以忽略不计时,我们就可以把物体看成质点
D.质点是一种特殊的实际物体
解析:质点不一定是很小的物体,只要物体的形状和大小在所研究的问题中属于无关因素或次要因素就能看成质点;相反的体积很小或质量很小的物体若是被研究的主体,也不能看成质点。
答案:C
平均速度:
质点在某段时间内的位移与发生这段位移所用时间的比值叫做这段时间(或位移)的平均速度v,即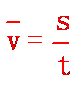 ,平均速度是矢量,其方向跟位移方向相同.平均速度是对变速运动的粗略描述。
,平均速度是矢量,其方向跟位移方向相同.平均速度是对变速运动的粗略描述。
瞬时速度:
运动物体在某一时刻(或经过某一位置)的速度,方向沿轨迹上质点所在点的切线方向指向前进的一侧,瞬时速度是对变速运动的精确描述,其大小叫速率。
平均速率:
物体在某段时间内通过的路程l跟通过这段路程所用的时间t的比值,叫做这段路程(或这段时间)的平均速率,即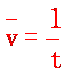 ,它是标量,值得注意的是:它并不是平均速度的大小.
,它是标量,值得注意的是:它并不是平均速度的大小.
平均速度和瞬时速度对比:
(1)区别:平均速度反映的是物体在整个运动过程中的整体运动情况,而瞬时速度反映的是物体在运动过程的某一时刻或某一位置的运动情况;
(2)联系:在匀速直线运动中,任何时刻的瞬时速度和整个运动过程中的平均速度相同。
方法与知识感悟:
平均速度是反映的某一段运动过程中的平均运动快慢,是这一过程中的位移与时间的比值( 是平均速度的定义式),适用于所有的运动;而
是平均速度的定义式),适用于所有的运动;而 适用于匀变速直线运动,但若
适用于匀变速直线运动,但若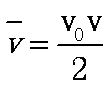 ,却不能判定该物体做匀变速直线运动.
,却不能判定该物体做匀变速直线运动.
平均速度的计算:
一辆汽车沿平直公路行驶,先以速度v1通过前的位移,再以速度v2=50km/h通过其余的位移.若整个位移中的平均速度=37.5km/h,则第一段位移内的平均速度是多少?
解:设整段位移为x,通过前位移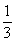 和后位移
和后位移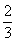 的时间分别为t和t
的时间分别为t和t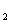 ,根据
,根据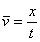 得
得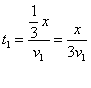 ,
,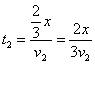 ,可得
,可得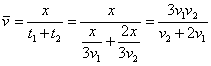 。解得第一段时间位移内的速度
。解得第一段时间位移内的速度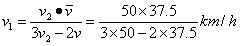 =25km/h。
=25km/h。
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的共同效果相同,这个力就叫做那几个力的合力,原来的几个力叫做这个力的分力。
①合力与分力是针对同一受力物体而言的。
②一个力之所以是其他几个力的合力,或者其他几个力之所以是这个力的分力,是冈为这一个力的作用效果与其他几个力共同作用的效果相当,合力与分力之间的关系是一种等效替代的关系。
③合力可能大于任何一个分力,也可能小于任何一个分力,也可能介于两个分力之间。
④如果两个分力的大小不变,夹角越大,合力就越小;夹角越小,合力就越大。
⑤两个大小一定的力F1、F2,其合力的大小范围
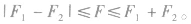

力的运算法则:
1.平行四边形定则
作用在同一点的两个互成角度的力的合力,不等于两分力的代数和,而是遵循平行四边形定则。如果以表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的对角线表示,这叫做力的平行四边形定则,如图所示。 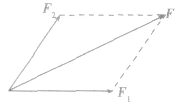
2.三角形定则和多边形定则如图(a)所示,两力F1、F2合成为F的平行四边形定则,可演变为(b)图,我们将(b)图称为三角形定则合成图,即将两分力F1、F2首尾相接,则F就是由F,的尾端指向F2的首端的有向线段所表示的力。
如果是多个力合成,则由三角形定则合成推广可得到多边形定则,如图为三个力F1,F2、F3的合成图,F 为其合力。
电荷、电荷守恒定律:
1.涉及电荷的基本概念
(1)电荷自然界中存在着两种电荷,它们分别为正电荷和负电荷。用毛皮摩擦过的橡胶棒上带的电荷叫负电荷,用丝绸摩擦过的玻璃棒上带的电荷叫正电荷。同种电荷互相排斥,异种电荷互相吸引。
(2)电荷量电荷量是指物体带电的多少。电荷量是电荷的定量量度。正电荷的电荷量为正值,负电荷的电荷量为负值。尽管电荷量有正、负值(正号一般省略),但要知道这里的“+”、“-”号代表电荷的性质(种类),与数学中的正、负号的含义不同。在国际单位制中,电荷量的单位是库仑,简称库,符号c。
(3)元电荷电子和质子带有等量的异种电荷,其电荷量e: 1.60×10-19C,称为元电荷,用e表示。所有带电体的电荷量都是元电荷e的整数倍,这就是说电荷量是不能连续变化的物理量。无电荷不是电荷,它是指电荷的电荷量,电荷量1.60×10-19C称为元电荷。元电荷的数值最早是由美国科学家密立根用实验测得的。所有带电体的电荷量等于元电荷或者等于元电荷的整数倍。质子、电子都不叫元电荷,它们电荷量的绝对值才叫元电荷。
(4)点电荷形状和大小对研究问题的影响可以忽略的带电体称为点电荷。
①点电荷是无大小、无形状、只有电荷量的一个理想化模型。在实际问题中,只有当带电体间的距离比它们自身的大小大得多,以至于带电体的形状和大小对相互作用力的影响可以忽略不计时,带电体才可以被视为点电荷。
②一个带电体能否被视为点电荷完全取决于自身的几何形状、大小与其他带电体之间的距离的比较。即带电体很小,不一定可被视为点电荷,带电体很大,也不一定不能被视为点电荷。
(5)感应电荷当一个带电体靠近导体时,南于电荷间相互吸引或排斥,导体中的自由电荷便会趋向或远离带电体,使导体靠近带电体的一端带异号电荷,远离带电体的一端带同号电荷。这种现象叫做静电感应。由于静电感应而使导体两端出现的等量异号电荷通常叫做感应电荷。其特点是:不带电导体靠近带电体时,靠近带电体的一端出现与带电体电性相反的电荷,远离带电体的一端出现与带电体电性相同的电荷。
(6)场源电荷电场是由电荷产生的,我们把产生电场的电荷叫做场源电荷。
(7)试探电荷研究电场的基本方法之一是在电场中放入一带电荷量很小的点电荷,分析其受力和能量情况,借以研究电场的性质,这样的电荷称为试探电荷。作为试探电荷的带电体,基本要求是体积要小,能研究电场中每一点的性质,还要求带电体所带电荷量要少.以放入试探电荷后试探电荷对原电场的影响可忽略为原则。
(8)净电荷物体带电实质是得到或失去了电子,讨论物体带何种电荷,所带电荷量是多少,是指物体的净电荷是正还是负,物体所具有的总电荷中正、负电荷的差值是多少,电荷量是物体中净电荷的多少。
(9)比荷带电体所带电荷量与其质量之比叫做该带电体的比荷。比荷是一个重要的物理量,常用来描述微观粒子的性质,在国际单位制中其单位为库仑每千克,符号 C/kg。
电场强度:


计算场强的四种方法:
1.计算电场强度的常用方法——公式法
(1)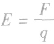 是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
(2)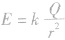 要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
(3)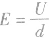 是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
2.计算多个电荷形成的电场强度的方法——叠加法
当空间的电场由几个点电荷共同激发的时候,空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和,其合成遵循矢量合成的平行四边形定则。
3.计算特殊带电体产生的电场强度的方法
(1)补偿法对于某些物理问题,当直接去解待求的A很困难或没有条件求解时,可设法补上一个B,补偿的原则是使A+B成为一个完整的模型,从而使A+B变得易于求解,而且,补上去的B也必须容易求解。这样,待求的A便可从两者的差值中获得,问题就迎刃而解了,这就是解物理题时常用的补偿法。用这个方法可算出一些特殊的带电体所产生的电场强度。
(2)微元法在某些问题中,场源带电体的形状特殊,不能直接求解场源带电体在空间某点所产生的总电场,此时可将场源带电体分割,在高中阶段,这类问题中分割后的微元常有部分微元关于待求点对称,这就可以利用场的叠加及对称性来解题。
4.计算感应电荷产生的电场强度的常用方法—— 静电平衡法根据静电平衡时导体内部场强处处为零的特点,外部场强与感应电荷产生的场强(附加电场)的合场强为零,可知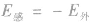 ,这样就可以把复杂问题变简单了。
,这样就可以把复杂问题变简单了。
与“物理学中用到大量的科学方法,建立下列概念时均用到“等效替代...”考查相似的试题有:
- 运动员取得百米短跑比赛的好成绩,取决于( )A.起跑时的速度大B.撞线时的冲刺速度大C.某段时间的平均速度大D.全程的平均...
- 北京奥运火炬实现了成功登上珠峰的预定目标,如图所示是火炬手攀登珠峰的线路图,请跟据此图判断下列说法正确的是[ ]A.由起...
- 不定项选择关于速度的说法正确的是( )A.速度与位移成正比B.平均速率等于平均速度的大小C.匀速直线运动任何一段时间内的...
- 2008年第8号台风“凤凰”于7月28日22时在福建省福清市东瀚镇沿海登陆。据江苏省气象台预报,风暴中心以18km/h左右的速度向西北...
- 小船在静水中的行驶速度是v,现在小船朝对岸垂直航行.当船行至河的正中间时,河水的流速突然增大一倍,则渡河时间比原来预定...
- 如图所示,质量为m的木块放在水平桌面上,木块与桌面间的动摩擦因数为μ,木块在水平推力F作用下匀速向右运动,当木块有1/4长...
- 如图所示,在水平力F的作用下,木块A、B保持静止.若木块A与B的接触面是水平的,且F≠0.则关于木块B的受力个数可能是( )A....
- 如图所示,将一个质量为1kg的小物块轻轻放上倾角为37°(sin37°=0.6)的斜面,已知斜面质量也为1kg,重力加速度为l0m/s2.斜面...
- 如图所示,一个质量分布均匀的球放在互成120°的两块光滑平面上保持静止状态OA是水平面,OB是倾斜面,关于球的受力,下列说法...
- 如图所示,ab是半径为R的圆的一条直径,该圆处于匀强电场中,场强为E、在圆周平面内,将一带止电q的小球从a点以相同的动能抛...