本试题 “福岛第一核电站核泄漏事故给日本环境带来了灾难,清除核污染已是迫在眉睫.(1)对于池塘水中的铯,可投入吸水性很强的沸石加以吸附.为测量一沸石块的密度,...” 主要考查您对浮力及阿基米德原理
质量的测量,天平的使用
体积的测量,量筒的使用
固体密度的测量
液体密度的测量
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 浮力及阿基米德原理
- 质量的测量,天平的使用
- 体积的测量,量筒的使用
- 固体密度的测量
- 液体密度的测量
(1)定义:浸在液体中的物体受到向上托的力叫做浮力。
(2)施力物体与受力物体:浮力的施力物体是液体 (或气体),受力物体是浸入液体(或气体)中的物体。
(3)方向:浮力的方向总是竖直向上的。
阿基米德原理:
(1)原理内容:浸在液体里的物体受到液体竖直向上的浮力,浮力的大小等于它排开的液体受到的重力。
(2)公式:
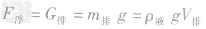 ,式中ρ液表示液体的密度,V排是被物体排开的液体的体积,g取9.8N/kg。
,式中ρ液表示液体的密度,V排是被物体排开的液体的体积,g取9.8N/kg。浮力大小跟哪些因素:
有关浸在液体中的物体受到浮力的大小,跟物体浸入液体中的体积有关,跟液体的密度有关,跟物体浸入液体中的深度无关。跟物体本身密度大小无关。
阿基米德原理的五点透析:
(1)原理中所说的“浸在液体里的物体”包含两种状态:一是物体的全部体积都浸入液体里,即物体浸没在液体里;二是物体的一部分体积浸入液体里,另一部分露在液面以上。
(2)G排指被物体排开的液体所受的重力,F浮= G排表示物体受到的浮力的大小等于被物体排开的液体的重力。
(3)V排是表示被物体排开的液体的体积,当物体全部浸没在液体里时,V排=V物;当物体只有一部分浸入液体里时,则V排<V物。
(4)由
 可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。
可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。(5)阿基米德原理也适用于气体,但公式中ρ液应该为ρ气。
控制变量法探究影响浮力大小的因素:
探究浮力的大小跟哪些因素有关时,用“控制变量法”的思想去分析和设计,具体采用“称量法”来进行探究,既能从弹簧测力计示数的变化中体验浮力,同时,还能准确地测出浮力的大小。
例1小明在生活中发现木块总浮在水面,铁块却沉入水底,因此他提出两个问题:
问题1:浸入水中的铁块是否受到浮力?
问题2:浮力大小与哪些因素有关?
为此他做了进一步的猜想,设计并完成了如图所示实验,
(1)(b)、(c)图中弹簧测力计示数均小于(a)图中弹簧测力计示数,说明浸入水中的铁块__(选填 “受到”或“不受到”)浮力;
(2)做___(选填字母)两次实验,是为了探究铁块浸没在水中时所受浮力大小与深度是否有关;
(3)做(d)、(e)两次实验,是为了探究浮力大小与 __的关系。
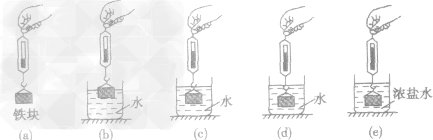
解析(1)物体在水中时受到水向上托的力,因此示数会变小。
(2)研究浮力与深度的关系时,应保持V排和ρ液不变,改变深度。
(3)在V排不变时,改变ρ液,发现浮力大小改变,说明浮力大小与ρ液有关。
答案(1)受到(2)(c)、(d)(3)液体密度
公式法求浮力:
公式法也称原理法,根据阿基米德原理,浸入液体中的物体受到向上的浮力,浮力的大小等于物体排开的液体受到的重力(表达式为:F浮=G排=ρ液gV排)。此方法适用于所有浮力的计算。
例1一个重6N的实心物体,用手拿着使它刚好浸没在水中,此时物体排开的水重是10N,则该物体受到的浮力大小为____N。
解析由阿基米德原理可知,F浮=G排=10N。
答案10
实验法探究阿基米德原理:
探究阿基米德原理的实验,就是探究“浮力大小等于什么”的实验,结论是浮力的大小等于物体排开液体所受的重力。实验时,用重力差法求出物体所受浮力大小,用弹簧测力计测出排开液体重力的大小,最后把浮力与排开液体的重力相比较。实验过程中注意溢水杯中的液体达到溢口,以保证物体排开的液体全部流入小桶。
例1在探究“浮力大小等于什么”的实验中,小明同学的一次操作过程如图所示。
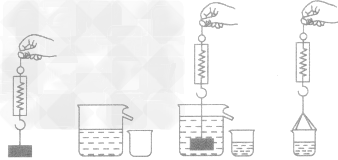
(1)测出铁块所受到的重力G铁;
(2)将水倒入溢水杯中;
(3)把铁块浸入溢水杯中,读出弹簧测力计示数F;
(4)测出小桶和被排开水的总重力G;
(5)记录分析数据,归纳总结实验结论,整理器材。
分析评估小明的实验,指出存在的问题并改正。
解析:在探究“浮力大小等于什么”的实验中,探究的结论是浮力的大小等于物体排开的液体所受到的重力,所以实验时,需要用弹簧测力计测出铁块受到的浮力和它排开水的重力进行比较得出结论,因此实验过程中需要测空小桶的重力G桶,并且将溢水杯中的水加至溢水口处。
答案:存在的问题:
(1)没有测空小桶的重力 (2)溢水杯的水量不足
改正:(1)测空小桶的重力G桶(2)将溢水杯中的水加至溢水口处
浮力知识梳理:

曹冲称象中的浮力知识:
例曹冲利用浮力知识,巧妙地测出了大象的体重。请你写出他运用的与浮力有关的知识_____、 ____,另外,他所用到的科学研究方法是:_____和______.
解析:曹冲称象的过程是首先把大象放在船上,在水面处的船舷上刻一条线,然后把大象牵上岸。再往船上放入石块,直到船下沉到船舷上的线再次与水面相平时为止,称出此时船上石头的质量即为大象的质量。两次船舷上的线与水面相平,根据阿基米德原理可知,为了让两次船排开水的体积相同,进而让两次的浮力相同,再根据浮沉条件,漂浮时重力等于浮力可知:船重+大象重=船重+石头重,用多块石头的质量替代了不可拆分的大象的质量,这是等效替代法在浮力中的一个典型应用。
答案:浮沉条件 阿基米德原理 等效替代法化整为零法
1.日常生活中常用的测质量工具,如图所示。
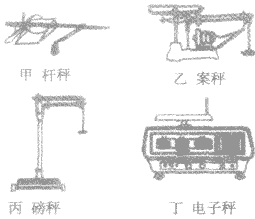
2.实验室常用工具:托盘天平和学生天平,如图所示。
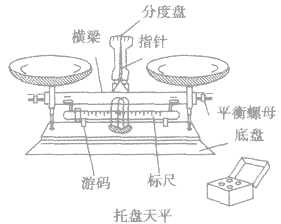
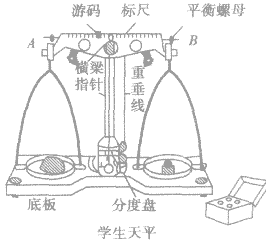
天平的使用方法:
在物理实验中,称量物体质量的工具是天平,为正确使用天平,需注意以下事项。
1.使用天平前需知
(1)了解天平的构造。天平由底盘、分度盘、横梁、平衡螺母、天平盘、标尺、游码、指针及砝码组成。
(2)知道天乎的称量和感量。学生天平的最大称量一般为200克;感量一般为0.2克。
2.天平的使用方法天平的使用方法可归纳为:放、移、调、称、读、收。
| 放 | 将天平放在水平台上 |
| 移 | 使用前将游码移至称量标尺左端的“0”刻线处 |
| 调 | 调节横梁上的平衡螺母,使指针指在分度盘的中央刻线处,这时横梁平衡。凋节平衡螺母的方法可归结为“螺母反指针”,也就是当指针向右偏,应将横梁上的平衡螺母向左调,即螺母调的方向与指针偏转的方向相反 |
| 称 | 称量时,把被测物体放在左盘,估计一下被测物体质量后,用镊子按“先大后小”的顺序向右盘中依次试加砝码,如果添加最小的砝码偏多,而取出这个最小的砝码又偏小,这时应取出最小的砝码,再调节游码在游码标尺上的位置,直到天平指针指在分度盘的中央刻线处.特别注意:被测物体和砝码的位置是“左物右码” |
| 读 | 右盘里砝码的总质量加上游码标尺上游码的示数值,就是被测物体的质量,即:m物=m砝+m游;游码的示数值以游码的左侧对齐格数为准;在使用天平时,若不小心按“左码右物”的方式放置,那么被测物体的质量应等于砝码质量之和减去游码在标尺上的示数值 |
| 收 | 测量完毕,把被测物体取下,砝码放回盒中,游码拨回标尺零刻度线处,即“取下物体,砝码回盒,游码回零” |
3.天平的使用可用以下口诀记忆
(1)天平先要放水平,游码左移要归零,旋转螺母针指中,左物右码要记清,砝码要用镊子取,湿、液要用容器称,先大后小移游码,渎数两码要相加。
(2)测质量,用天平,先放平,再调平,游码左移零,螺母来调平,左物右码要记清,先大后小镊取码,平衡质量加游码。
使用天平常见的问题
1.游码未归零问题
题型特征:游码未置于标尺左端的零刻度线处就将天平调节平衡了,而在称量的过程中又移动了游码的位置。游码在天平的使用过程中的作用相当于一个其数值可以变化的小砝码,只要游码位置不动,就没有起到小砝码的作用.因而物体的质量与游码位置无关。但当游码移动时,情况就发生了变化,在正常使用情况下,将游码向右移动,相当于在右盘中添加砝码;同理,若将游码向左移动,则相当于在左盘中添加砝码(或者相当于在右盘中减去砝码)。
2.物码错位问题
题型特征:称量时误将被测物体和砝码位置放反。正常情况下,物体(质量为m物)放在天平左盘,砝码(质量为m码)放在天平右盘,且游码(质量为m游)是作为小砝码在使用的,所以有m左=m右即m物=m码+ m游;若物码错位放置,则等式为m码=m物+m游,即被测物体的质量m物=m码一m游。
3.砝码不规范问题
如果砝码磨损,其质量减小,用它来平衡与它示数相同的物体,必须向有移动游码,因此,读出的数值是砝码示数加上游码所对的刻度值,它比物体质量大。如果砝码上粘有其他物质,砝码的质量比它的实际质量大,称量时,导致游码向右移动较少,读出的数值比物体的实际质量小。
天平使用时的几个为什么
1.观察天平是否平衡。为什么要采用“摆动法”?
答:无论是调节天平空载时的零点,还是称量过程中观察天平是否平衡,一般都采用横梁“摆动法”,这主要是为了克服天平的摆动惯性。尽管指针在分度盘上左有摆动的幅度会依次递减,但只要指针两边摆动的幅度基本相等,便可认为天平达到平衡。
2.使用天平时为什么要强调物体必须放在左盘中,砝码放在右盘中?
答:我们知道,空载时天平调平后,游码在标尺的最左端零刻度处;称量时,游码要向右移动。这时,游码所示的质量加上右盘中的砝码的质量,就等于被测物体的质量,即m物=m砝+m游。如果将物体放在右盘中,将砝码放在左盘中,游码所示的质量加上砝码的质量就不等于被测物体的质量,而是游码的质量加被测物体的质量等于砝码的质量,即m砝=m物+m游。因此,这样称量,按常规方法读数,结果会偏大(这时被测物体的质量应为m物=m砝-m游)。因此,使用天平测质量时,物体要放在左盘中,砝码要放在右盘中。
3.为什么使用天平称物体的质量时,被测物体的质量不能超过它的称量?
答:每一种测量工具都有一个测量范围,天平也一样。天平的称量就是它所配备的所有砝码的质量再加上标尺上最大刻度值的质量。如果被测物体的质量超过了这个称量,显然天平不可能平衡,闪而测不出结果。其次,仔细观察天平横梁的支点,就会发现它是一个十分锋利的刀口。如果被测物体的质量超过了天平的称量,就会损伤刀口,使天平摆动不灵活,影响测量的准确性。因而使用天平时,不能测超过它称量的物体。用镊子加减砝码时要轻拿轻放,也是为了避免损伤刀口及其他部件。
体积表示物体所占空间的大小,用字母V,来表示。
体积的单位也采用国际制单位,有立方米(m3)、立方分米(dm3)、立方厘米(cm3)。换算关系为:1m3= 1000dm3:1dm3=1000cm3;1m3=106cm3。
容积:
容积是指容器内部窄间的大小,容积单位有升 (L)、毫升(mL)。
换算关系为:1L=1000mL。与体积单位的对应关系是1L=1dm3;1mL=1cm3。
量筒:
1. 量筒的使用:
①量筒的规格量筒是用来量取液体体积的一种玻璃仪器,一般规格以所能度量的最大容量(mL)表示,常用的有10mL,20mL,25mL,50mL,100mL,250mL、500mL,1000mL等多种规格。
②量筒的选择方法:
量筒外壁刻度都是以mL为单位。10mL量筒每小格表示0.1mL,而50mL量筒有每小格表示1mL或0.5mL的两种规格。可见,绝大多数的量筒每小格是量筒容量的1/100,少数为1/50。
量筒越大,管径越粗,其精确度越小,由视线的偏差所造成的读数误差也就越大。
所以,实验中应根据所取溶液的体积,尽量选用能一次量取的最小规格的量筒。分次量取会引起较大误差。如量取70mL液体,应选用100mL量筒一次量取,而不能用10mL量筒量取7次。
③液体的注入方法
向量筒里注入液体时,应用左手拿住量筒,使量筒略倾斜,右手拿试剂瓶,标签对准手心。使瓶口紧挨着量筒口,让液体缓缓流入,待注入的量比所需要的量稍少(约差1mL)时,应把量筒水平正放在桌面上,并改用胶头滴管逐滴加入到所需要的量。
④量筒的刻度
量筒没有“0”刻度,“0”刻度即为其底部。一般起始刻度为总容积的1/10或1/20。例如:10mL量筒一般从0.5mL处才开始有刻度线,所以,我们使用任何规格的量筒都不能量取小于其标称体积数的1/20以下体积的液体,否则,误差太大。应该改用更小的合适量筒量取。
在实验室做化学实验时,量筒的刻度面不能背对着自己,这样使用起来很不方便。因为视线要透过两层玻璃和液体,不容易看清。若液体是浑浊的,就更看不清刻度,而且看刻度数字也不顺眼,所以刻度面正对着自己为好。
⑤读取液体的体积方法
注入液体后,要等一会,使附着在内壁上的液体流下来,再读取刻度值。否则,读出的数值将偏小。
读数时,应把量筒放在平整的桌面上,观察刻度时,视线、刻度线与量筒内液体的凹液面最低处三者保持水平,再读出所取液体的体积数。否则,读数会偏高或偏低。
⑥关于量筒仰视与俯视的问题
在看量筒的容积时是看液面的中心点
仰视时视线斜向上视线与筒壁的交点在液面下所以读到的数据偏低,实际值偏高。
俯视时视线斜向下视线与筒壁的交点在液面上所以读到的数据偏高,实际值偏低。

2. 注意事项
①量筒面上的刻度是指室内温度在20℃时的体积数。温度升高,量筒发生热膨胀,容积会增大。由此可知,量筒是不能加热的,也不能用于量取过热的液体,更不能在量筒中进行化学反应或配制溶液。
②量筒一般只能用于要求不是很严格时使用,通常可以应用于定性分析和粗略的定量分析实验,精确的定量分析是不能使用量筒进行的,因为量筒的误差较大,此时可用移液管或滴定管来代替。
③从量筒中倒出液体后是否要用水冲洗要看具体情况而定。如果是为了使所取的液体量更准确,似乎要用水洗涤后并把洗涤液倒入所盛液体的容器中,这是不必要的。因为在制造量筒时已经考虑到有残留液体这一点;相反,如果洗涤反而使所取体积偏大。如果是用同一量筒再量别的液体,这就必须用水冲洗干净并干燥,为防止相互污染。
④10mL的量筒一般不需读取估读值。因为量筒是粗量器,并且又是量出仪器,在倒出所量取的液体时,总会有1~2滴(1滴相当于0.05mL)附着在内壁上而无法倒出,其相差的体积大小已经和其最小刻度差相同,所以估读值再准确也无多大意义,只需读取到0.1mL。
规格大于10mL的量筒一般需要读取估读值,若不读取,误差反而更大。因此,无论多大规格的量筒,一般读数都应保留到0.1mL
3. 量筒的使用要做到“五会”
①会选。任何一只量筒都有一定的测量范围,即量程,要能根据被测量的量选择量程合适的量筒。
②会放。使用量筒测量时,量筒要平稳地放置于水平桌面上。
③会看。读取量筒的数据时,若液面是凹液面,视线应以凹液面底部为准;若液面是凸液面,视线应以凸液面顶部为准。
④会读。要会根据量筒刻度的分度值读出准确值,同时要读出分度值的下一位,即估计值。
⑤会用。
测体积的方法:
①用量筒直接测液体体积;
②规则形状的物体可用刻度尺测出相关长度,算出体积;
③用代替法可测不规则形状容器的容积。先将容器灌满水,然后将水倒入量筒中即可测其容积;
④用量筒、水、细线可测密度比水大的固体体积。具体步骤是:在量筒中加入适量的水,记下水的体积V0;用细线系住物体并轻轻放入量筒中,记下此时水和物体的体积为V1;物体的体积V=V1-V0。用量筒测固体的体积,采取的是“排液法”,依据的是等量替代;
⑤形状不规则、且漂浮在液体上的固体的体积的测量,可用非常规的办法测量。由于物体漂浮于液面,可以用“针压法”,也就是用一枚细针将漂浮物压入液体中;或用一密度比液体密度大得多且不溶于液体的物体将漂浮物拉入水中,此法称为“助沉法”。如用量筒、水、细针(或细线、铁块)可测密度比水小的固体的体积。
原理:由密度公式
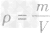 可知,要测量某种物质的密度,需要测量由这种物质构成的物体的质量的体积。
可知,要测量某种物质的密度,需要测量由这种物质构成的物体的质量的体积。测量方法:
1. 形状规则的固体:质量可用天平测量,体积可直接用刻度尺测长、宽、高等,并利用体积公式算出,如正方体的体积V=a3,圆柱体的体积V=πr2h,长方体的体积V=abc,根据
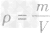 求得密度。
求得密度。2. 形状不规则的固体(不溶于水):
(1)体积可用“排水法”间接测出
(2)质量可用天平测量
①先在量筒中倒入适量水,读出水的体积V1(水的多少以刚好淹没固体为宜。水过多,放入固体后液面会超过量程;水过少,不能淹没固体)
②将固体用细线拴住慢慢放人量筒内水中,并使其全部淹没,此时读出水与固体的总体积V2
③由V=V2-V1,得出固体体积。
最后根据
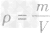 求得密度。
求得密度。Ⅰ方法一:天平量筒法
例:有一块形状不规则的石块,欲测量它的密度,所需哪些器材并写出实验步骤,并表示出测量的结果。
分析:用天平和量筒测定密度大于水的物质的密度,可用排水法测体积。
实验原理: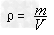
实验器材:天平(砝码)、量筒、烧杯、滴管、线、水、石块
实验步骤:
(1)用调节好的天平,测出石块的质量m;
(2)在量筒中倒入适量的水,测出水的体积V1;
(3)将石块用细线拴好,放在盛有水的量筒中,(排水法)测出总体积V2;
实验结论:ρ=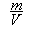 =
=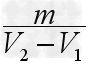 。
。
Ⅱ方法二:助沉法
例:有一块形状不规则的蜡块,欲测量它的密度,所需哪些器材并写出实验步骤,并表示出测量的结果。
分析:用天平和量筒测定密度小于水的物质的密度,可用助沉法测体积。
实验原理: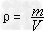
实验器材:天平(砝码)、量筒、烧杯、滴管、线、水、蜡块、铁块。
实验步骤:
(1)用调节好的天平,测出蜡块的质量m;
(2)在量筒中倒入适量的水,如图甲将蜡块和铁块用细线拴好,先将测铁块没入水中,测出水和石块的体积V1
(3)再将蜡块浸没在水中,如图乙。(助沉法)测出水、石块、蜡块的体积总体积V2;
实验结论: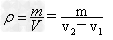
注意:物质的密度比水小,放在量筒的水中漂浮,不能直接用量筒测出体积。例题中采用的方法是助沉法中的沉锤法,还可以用针压法,即用一根很细的针,将物体压入量筒的水中,忽略细针在水中占据的体积,则可用排水法直接测出物体的体积了。
Ⅲ方法三:等浮力法
例:小明家买的某品牌的牛奶喝着感觉比较稀,因此他想试着用学过的知识测量一个这种牛奶的密度。他先上网查询了牛奶的密度应该为1.03g/cm3,然后他找来一根粗细均匀的细木棒,在木棒的表面均匀地涂上一层蜡,并在木棒的一端绕上一段金属丝(体积不计),做成了一枝“密度计”,小明又找来一个足够深的盛水容器和一把刻度尺,请你帮助小明利用这些器材设计一个测量牛奶密度的方案。要求写出主要的测量步骤并推导出计算牛奶密度的公式(有足量的水和牛奶)。
实验原理:漂浮条件、阿基米德原理。
实验器材:刻度尺、粗细均匀的细木棒、一段金属丝、烧杯、水、牛奶。
实验步骤:
(1)将一段金属丝绕在木棒的一端,制成“密度计”,用刻度尺测出其长度L;
(2)将“密度计”放入盛有水的烧杯中,使其漂浮在水中,用刻度尺测出“密度计”露出水面的高度h水;
(3)将“密度计”放入盛有牛奶的烧杯中,使其漂浮在牛奶中,用刻度尺测出“密度计”露出牛奶液面的高度h牛。
实验结论:因为“密度计”在水中和在牛奶中,均处于漂浮状态。因此“密度计”在水中和在牛奶中受到的浮力都等于“密度计”的重力。“密度计”的重力不变,所以两次浮力相等。即F牛=F水,根据阿基米德原理可得:
ρ牛gV牛排=ρ水gV水排
ρ牛gSh牛排=ρ水gSh水排
∵h牛排=L-h牛h水排=L-h水
∴ρ牛(L-h牛)=ρ水(L-h水)
牛奶的密度: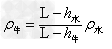
注意:从给定的器材看,即无量筒,也无天平,此时解题的着眼点就不能局限于利用质量、体积测密度。应该展开丰富的联想,而给出“密度计”,是和浮力有关的,就要联想到利用浮力测液体的密度。这种利用两次浮力相等来测密度,我们简称为“等浮力法”。
Ⅳ弹簧测力计法(也可称双提法)
例:张小清同学捡到一块不知名的金属块,将它放到水中可以沉没,现在,小清同学想测出它的密度,但身边只有一支弹簧秤、一个烧杯及足量的水,请你帮她想一想,替她设计一个测量金属块密度的实验过程,写出实验步骤
分析与解:
这是一道典型的利用浮力知识测密度的试题。阿基米德原理的重要应用就是已知浮力求体积。它的基本思路就是用弹簧测力计测出浮力,利用水的密度已知,求得物体的体积,即可计算出物体的密度值。
实验原理:阿基米德原理
实验器材:一支弹簧秤、一个烧杯及足量的水、金属块、线。
实验步骤:
(1)用细线系住金属块,在烧杯中倒入适量的水;
(2)用弹簧测力计测出金属块受到的重力G;
(3)用弹簧测力计测出金属块浸没在水中受到的拉力F。
实验结论:
注意:利用弹簧测力计提着金属块测一次重力;再提着金属块测一次金属块在水中时弹簧测力计的拉力。因此简称为双提法。这一实验使用的仪器少,操作简单,是常用的测量物体密度的方法。
原理:由密度公式
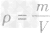 可知,要测量某种物质的密度,需要测量由这种物质构成的物体的质量的体积。
可知,要测量某种物质的密度,需要测量由这种物质构成的物体的质量的体积。测量方法:
液体的体积可用直接用量筒(或量杯)测出,其质量就要通过“质量差法”来测定,即先称出容器的质量,再称出容器与液体的总质量,两者之差就是倒入容器内液体的质量,再根据
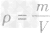 求得密度。
求得密度。液体密度测量方法:
一、常规法:
器材:烧杯、量筒、天平、待测液体
步骤:
1.用天平称出烧杯的质量M1;
2.将待测液体倒入烧杯中,测出总质量M2;
3.将烧杯中的液体倒入量筒中,测出体积V;
4.计算表达:ρ=(M2-M1)/V
二、等容法
器材:烧杯、水、待液体、天平。
步骤:
1.用天平称出烧的质量M1;
2.往烧杯内倒满水,称出总质量M2;
3.倒去烧杯中的水,往烧杯中倒满待测液体,称出总质量M3;
4.计算表达:ρ=ρ水(M3-M1)/(M2-M1)
三、浮力法
器材:弹簧秤、水、待测液体、小石块、细绳子
步骤:
1.用细绳系住小石块,用弹簧秤称出小石块的重力G;
2.将小块浸没入水中,用弹簧秤称出小石的视重G1;
3.将小块浸没入待测液体中,用弹簧秤称出小石块的视重G2;
4.计算表达:ρ=ρ水(G-G2)/(G-G1)
四、压强法
用刻度尺、两端开口的直玻璃管(一端有橡皮膜)、烧杯、适量的水、足量的牛奶、细线。计一种测量奶密度的方法。
实验步骤:
1.在玻璃管内倒入一定深度的牛奶;
2.将管竖直放入水中,带橡皮膜水平时,用刻度尺量出管底到牛奶面和水面的深度,分别为h1、h2;
3.根据p1=p2得表达式:ρ牛奶=h2ρ水/h1
五、U形管法:
器材:U形管、水、待测液体、刻度尺步骤:
1.将适量水倒入U形管中;
2.将待测液体从U形管的一个管口沿壁缓慢注入;
3.用刻度尺测出管中水的高度h1,待测液体的高度h2;
4.计算表达:ρ=ρ水h1/h2 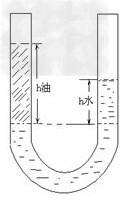
(用此种方法的条件是:待测液体不溶于水,待测液体的密度小于水的密度)
六、密度计法:
器材:密度计、待测液体
方法:将密度计放入待测液体中,直接读出密度。
与“福岛第一核电站核泄漏事故给日本环境带来了灾难,清除核污染...”考查相似的试题有:
- 深圳号导弹驱逐舰是我国现代化的现役新型导弹驱逐舰,该舰满载排水量6600吨,它满载时所受到的浮力大小为:______N,它从海口...
- 在研究浮力问题时,某同学做了如图实验,则实验中F1、F2、F3、F4的关系是[ ]A.F1=F2=F3=F4B.F1=F2=F4-F3C.F1=F2、F3=F4D.F1-F...
- 一艘轮船从海里驶入河里,下列说法正确的是( ______)A.轮船所受浮力变小 B.轮船所受浮力变大C.轮船排开液体的体积变小 D...
- 在南极考察中使用的海洋破冰船,针对不同的冰层有不同的破冰方法.其中一种破冰方法是:接触冰面前,船全速航行,船体大部分...
- 一个重15N,体积为1dm3的小球,用手抓住将它浸没在水中,它受到的浮力是 ______N;松手后小球将 ______(填“上浮”“下沉”或“悬...
- 如图所示,是一位先生巧用物理知识用气球将帽子送给楼上女士的情景。此过程中应用的关键知识是:[ ]A.气球受到重力B.帽子质量...
- 在研究物体浮沉条件实验中,将鸡蛋放入装有水的玻璃杯中后下沉入水底.为了使鸡蛋上浮,可采用的措施是向杯中加入适量的( )...
- 调节天平时,首先将天平放在水平桌面上,再把游码移到标尺的零刻线处,若指针静止时指在分度盘的右侧,这时应将平衡螺母向___...
- 在使用天平测量物体质量时,称量过程中横梁左侧偏高,下列操作不当的是( )A.减少砝码B.向左调节平衡螺母C.把较大的砝码...
- 如图,弹簧测力计的读数是_________N;物体A的体积为_________cm3;