热平衡方程：
在热传递过程中，如果没有热量损失，则高温物体放出的热量Q_放等于低温物体吸收的热量Q_吸，即Q_放=Q_吸，把这个关系叫热平衡方程。
热平衡方程式：
    两个温度不同的物体放在一起，高温物体放出热量，低温物体吸收热量，当两个物体温度达到相同时，如果没有热量损失，则有Q_吸=Q_放，称为热平衡方程。在热量计算题中，常采用此等式。
例1：吃早饭的时候，妈妈用热水给小雪加热如图所示的袋装牛奶。为了使这袋牛奶的温度由 12℃升高到42℃，妈妈至少要用 60℃的热水多少千克?[水的比热容为4．2×10³J／(kg·℃)，设该牛奶的比热容为2．5 ×10³J／(kg·℃)，不计热量损失]


解析：根据热传递的条件，热水的最终温度等于牛奶的最终温度，同为42℃，由于不计热量损失，所以牛奶吸收的热量Q_吸等于热水放出的热量Q_放，根据Q_吸=Q_放即可求出。
牛奶升温时吸收的热量 Q_放=c₁m₁(t一t₀)=2．5×10³J／(kg·℃)× 0．25kg×(42℃-12℃)=18750J，
热水由60℃降低到42℃放出的热量 Q_放=c₂m₂(t₀’一t)，Q_吸=Q_放，

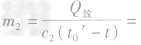
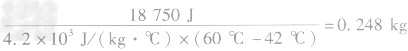
至少需要60℃的热水约0．248kg。

电功计算基本公式及推导公式（适用于纯电阻电路）：W=UIt，W=I²Rt，W=U²t/R，W=Pt，W=Uq。
电功计算：
1. W=UQ_电
电能也是一种能量，而这种能量的实施者就是电荷，电荷量就是这种能量在一般的时间内所有参与作功从A点到B点的实行者，每个电荷从A点到B点做的功就是电压，两者相乘就是AB的电功，就是消耗的电能

2. W=UIt
我们来看一下电功的含义，电功通俗的讲就是AB之间的一段时间A点到B点所消耗的电能（A点到B点可以是一个用电器，也可以是一部分电路）电压的实质是一个单位的电荷从A点到B点所做的功，电流提供的是在一个单位时间内AB之间的电荷量，时间也有了，那么AB之间的电荷量在一定时间内从A点到B点所做的功也就是消耗的电能就是W=UIt

3. W=Pt
W_电功、P_电功率、t_时间
像功的计算方法一样就是功率乘以时间，在生活中可以理解为工作总量=工作效率×工作时间，同样道理电所做的功当就等于电做功的效率乘以时间

W=I²Rt　（纯电阻电路）

密度公式的应用：
（1）利用m=ρV求质量；利用V=m/ρ求体积

（2）对于密度公式，还要从以下四个方面理解
①同种物质，在一定状态下密度是定值，它不随质量大小或体积大小的改变而改变。当其质量（或体积）增大几倍时，其体积（或质量）也随着增大几倍，而比值是不变的。因此，不能认为物质的密度与质量成正比，与体积成反比；
②具有同种物质的物体，在同一状态下，体积大的质量也大，物体的体积跟它的质量成正比；
③具有不同物质的物体，在体积相同的情况下，密度大的质量也大，物体的质量跟它的密度成正比；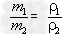

④具有不同物质的物体，在质量相同的条件下，密度大的体积反而小，物体的体积跟它的密度成反比。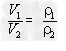

密度公式的应用：
1. 有关密度的图像问题
此问题一般是给出质量一体积图像，判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值，然后在纵坐标(或横坐标)上找到对应的数值，进行分析比较。
 例1如图所示，是甲、乙两种物质的m一V图像，由图像可知(   )
A．ρ_甲>ρ_乙
B．ρ_甲=ρ_乙
C．ρ_甲<ρ_乙
D．无法确定甲、乙密度的大小

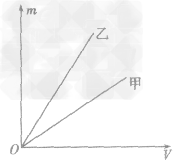
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到，我们要先借助图像，根据公式ρ =总结规律后方可。
如图所示，在横轴上任取一点V₀，由V₀作横轴的垂线V₀B，分别交甲、乙两图线于A、B两点，再分别从A、B两点作纵轴垂线，分别交纵轴于m_甲、m_乙两点。则甲、乙两种物质的密度分别为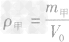，ρ_乙= 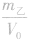，因为m_甲<m_乙，所以ρ甲<ρ乙，故C正确。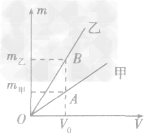

2. 密度公式ρ =及变形、m=ρV的应用：
密度的公式是ρ =，可得出质量计算式m=ρV 和体积计算式。只要知道其中两个物理量，就可以代入相应的计算式进行计算。审题时注意什么量是不变的，什么量是变化的。
例2某瓶氧气的密度是5kg/m³，给人供氧用去了氧气质量的一半，则瓶内剩余氧气的密度是_____；容积是10L的瓶子装满了煤油，已知煤油的密度是 0．8×10³kg/m³，则瓶内煤油的质量是_____，将煤油倒去4kg后，瓶内剩余煤油的密度是______。
 解析：氧气用去一半，剩余部分仍然充满整个氧气瓶，即质量减半体积不变，所以氧气的密度变为 2．5kg/m³。煤油倒去一半后，体积质量同时减半，密度不变。
答案：2．5kg/m³；8kg；0．8×10kg/m³。

3. 比例法求解物质的密度
   利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是：题目所描述的物理现象，由初始状态到终结状态的过程中至少有一个量保持不变，这个不变的量是由初始状态变成终结状态的桥梁，我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3：2，体积之比为l：3，那么它们的密度之比为(   )
A．1：2B．2：1C．2：9D．9：2
解析：（1）写出所求物理量的表达式：，
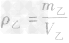
（2）写出该物理量比的表达式：

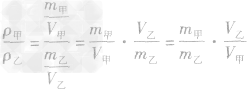
（3）化简：代入已知比值的求解：


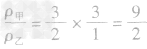
密度、质量、体积计算中的“隐含条件” 问题：
  很多物理问题中的有些条件需要仔细审题才能确定，这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例，密度计算题形式多样，变化灵活，但其中有一些题具有这样的特点：即质量、体积、密度中的某个量在其他量发生变化时保持不变，抓住这一特点，就掌握了求解这类题的规律。

1．隐含体积不变
例1一个瓶子最多能装0．5kg的水，它最多能装_____kg的水银，最多能装_____m³的酒精。 ρ水银=13．6×10³kg／m³，ρ水=1．0×10³kg／m³，ρ酒精= 0．8×10³kg／m³)
解析:最多能装即装满瓶子，由最多装水量可求得瓶子的容积为V=5×10^-4m³，则装水银为m_水银=13．6×10³kg／m³×5×10^-4m³=6．8kg。装酒精的体积为瓶子的容积。
答案6．8；5×10^-4

2. 隐含密度不变
例2一块石碑的体积为V_样=30m³，为测石碑的质量，先取了一块刻制石碑时剔下来的小石块作为样品，其质量是m_样=140g，将它放入V₁=100cm³的水中后水面升高，总体积增大到V₂=150cm³，求这块石碑的质量m_碑。
解析：此题中隐含的条件是石碑和样品是同种物质，密度相同，而不同的是它们的体积和质量。依题意可知，样品体积为：
V_样=V₂-V₁=150cm³一100cm³=50cm³ =5．0×10^-5m³
得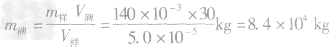=84t
答案：84t

3. 隐含质量不变
例3质量为450g的水结成冰后，其体积变化了 ____m3。(ρ水=0．9×10³kg／m³)
解析：水结成冰后，密度减小，450g水的体积为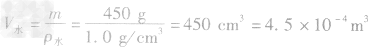，水结成冰后，质量不变，因此冰的体积为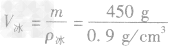=500cm³=5．0×10^-4m³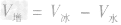，=5．0× 10^-4m³一4．5×10^-4m³=5×10^-5m³。

合金物体密度的相关计算：
     首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征，然后根据具体问题，灵活求解。
例两种不同的金属，密度分别为ρ1、ρ2：
(1)若墩质量相等的金属混合后制成合金，则合金的密度为____。
(2)若取体积相等的金属混合后制成合金，则合金的密度为_____。
解析：这道题的关键是抓住“两总”不变，即总质量和总体积不变。在(1)中，两种金属的质量相等，设为m1=m2=m，合金的质量m_总=2m，则密度为ρ1的金属的体积V1=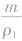，密度为ρ2的金属的体积V2=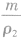，合金的体积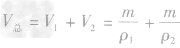，则合金的密度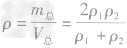
在（2）中两种金属的体积相等，设为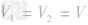，合金的体积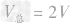，密度为ρ1的金属的质量m1=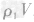，密度为ρ2的金属的质量为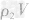，合金的质量m总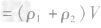，合金的密度为。
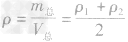答案：
注意：上述规律也适用于两种液体的混合，只要混合液的总质量和总体积不变即可。