本试题 “小汽车从静止开始以1m/s2的加速度前进,小汽车后面距离车25m处,某人同时开始以6m/s的速度匀速追车,试分析人是否能追上小汽车?如追不上,求人、车间的最...” 主要考查您对匀速直线运动
匀变速直线运动规律的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 匀速直线运动
- 匀变速直线运动规律的应用
定义:
在任意相等的时间内位移相等的直线运动叫做匀速直线运动。
特点:
加速度a=0,速度v=恒量。
位移公式:
S=vt。
知识点拨:
- 匀变速直线运动是在相等时间内速度变化相等的直线运动。注意在此定义中所涉及的“相等时间内”应理解为任意相等的时间内,而非一些特定相等的时间内。
- 做匀速直线运动的物体在任意相同时间内通过的路程都相等,即路程与时间成正比;速度大小不随路程和时间变化;位移与路程的大小相等。

- 匀速直线运动是理想状态与实际的结合。匀速直线运动不常见,因为物体做匀速直线运动的条件是不受外力或者所受的外力和为零,但是我们可以把一些运动近似地看成是匀速直线运动。如:滑冰运动员停止用力后的一段滑行、站在商场自动扶梯上的顾客的运动等等。我们可用公式v=s/t求得他们的运动速度。式中,s为位移,v为速度且为恒矢量,t为发生位移s所用的时间。由公式可以看出,位移是时间的正比例函数:位移与时间成正比。
- 当物体处于匀速直线运动时,物体受力平衡。
- 做匀速直线运动的物体其速度是保持不变的,因此,如果知道了某一时刻(或某一距离)的运动速度,就知道了它在任意时间段内或任意运动点上的速度。
基本公式:
①速度公式:vt=v0+at;
②位移公式:s=v0t+ at2;
at2;
③速度位移公式:vt2-v02=2as。
推导公式:
①平均速度公式:V=![]() 。
。
②某段时间的中间时刻的瞬时速度等于该段时间内的平均速度:![]() 。
。
③某段位移的中间位置的瞬时速度公式:![]() 。无论匀加速还是匀减速,都有
。无论匀加速还是匀减速,都有![]() 。
。
④匀变速直线运动中,在任意两个连续相等的时间T内的位移差值是恒量,即ΔS=Sn+l–Sn=aT2=恒量。
⑤初速为零的匀变速直线运动中的比例关系(设T为相等的时间间隔,s为相等的位移间隔):
Ⅰ、T末、2T末、3T末……的瞬时速度之比为:v1:v2:v3:……:vn=1:2:3:……:n;
Ⅱ、T内、2T内、3T内……的位移之比为:s1:s2:s3:……:sn=1:4:9:……:n2;
Ⅲ、第一个T内、第二个T内、第三个T内……的位移之比为:sⅠ:sⅡ:sⅢ:……:sN=1:3:5:……:(2N-1);
Ⅳ、前一个s、前两个s、前三个s……所用的时间之比为:t1:t2:t3:……:tn=1:![]() ……:
……:![]() ;
;
Ⅴ、第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ:……:tN=1:![]() ……:
……:![]() 。
。
追及相遇问题:
①当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距会越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题。
②追及问题的两类情况:
Ⅰ、速度大者减速(如匀减速直线运动)追速度小者(如匀速运动): 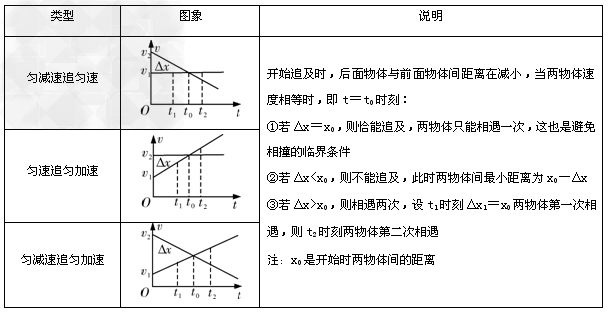
Ⅱ、速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):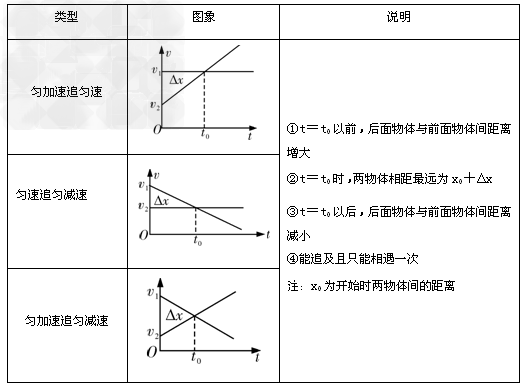
③相遇问题的常见情况:
Ⅰ、同向运动的两物体追及即相遇;
Ⅱ、相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇。
知识点拨:
例:如图所示,光滑斜面AE被分为四个长度相等的部分,即AB=BC=CD=DE,一物体由A点静止释放,下列结论不正确的是( )
A. 物体到达各点的速率之比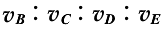 =
=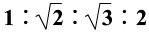 。
。
B. 物体到达各点所经历的时间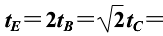
 。
。
C. 物体从A运动到E的全过程的平均速度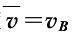 。
。
D. 物体通过每一部分时,其速度增量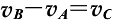
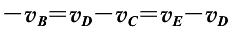 。
。
解析:由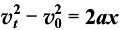 及
及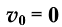 得
得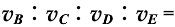
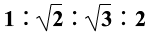 ,即A正确。由
,即A正确。由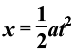 得
得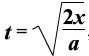 ,则
,则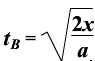 ,
, ,
,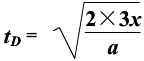 ,
,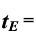
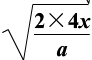 ,由此可知B正确。由
,由此可知B正确。由 得
得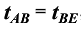 ,即B点为AE段的时间中点,故
,即B点为AE段的时间中点,故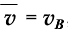 ,即C正确。对于匀变速直线运动,若时间相等,速度增量相等,故D错误,只有D符合题意。
,即C正确。对于匀变速直线运动,若时间相等,速度增量相等,故D错误,只有D符合题意。
答案:D
与“小汽车从静止开始以1m/s2的加速度前进,小汽车后面距离车25m...”考查相似的试题有:
- 车从静止开始以1m/s2的加速度前进,车后相距 x0=25 m处,与车运动方向相同的某人同时开始以6m/s的速度匀速追车,问能否追上?...
- “神舟”六号运行在距地面约343km的圆形轨道上时,航天员费俊龙在飞船内连续做了四个漂亮的前滚翻动作,历时约3min.若已知地球...
- 第四次提速后,出现了“星级列车”。从其中的T14次列车的时刻表可知,列车在蚌埠至济南区间段运行过程中的平均速率为( )T14次...
- 甲火车正以速率v1向前行驶,司机突然发现正前方同一轨道上距离为s处有另一火车乙,正以较小的速率v2沿同方向做匀速运动,甲车...
- 看下图回答问题
- 、为了安全,汽车过桥的速度不能太大。一辆汽车由静止出发做匀加速直线运动,用10s时间通过一座长120m的桥,过桥后的速度是14...
- 一辆汽车由静止开始做匀加速直线运动,下列说法正确的是( )A.在1秒内、2秒内、3秒内的位移之比是1:3:5B.第1秒末、第2秒...
- 如图所示,质量为m1=50kg的某学生(可视为质点)站在长为L=3m、质量为m2=100kg的甲车右端,人和车均处于静止状态,地面水平光...
- 一质点做直线运动的位移与时间的关系为(各物理量均采用国际单位制单位),则该质点( )A.第1s内的位移是6mB.前2s内的平均...
- 如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别...