平均速度公式：
V=。

某段时间的中间时刻的瞬时速度等于该段时间内的平均速度：
。
某段位移的中间位置的瞬时速度公式：
。无论匀加速还是匀减速，都有。

匀变速直线运动中，在任意两个连续相等的时间T内的位移差值是恒量，即ΔS=S_n+l–S_n=aT²=恒量。

初速度为零的匀加速直线运动的几个比例关系推导：

初速度为零的匀加速直线运动(设其为等分时间间隔)：
① t秒末、2t秒末、……nt秒末的速度之比：(V_t=V₀+at=0+at=at)V₁：V₂：V₃……V_n=at：a2t：a3t…：ant=1：2：3…：n
②前一个t秒内、前二个t秒内、……前N个t秒内的位移之比：S₁=v₀t+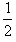at²=0+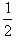at²=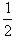at²；S₂=v₀t+a(2t)²=2at²；S₃=v₀t+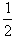at²=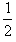a(3t)²=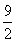at²；S_n=v₀t+at²=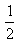a(nt)²=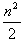at²。S₁：S₂：S₃…….S_n=at²：2at²：at²……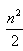at²=1：2²：3²….N^2
③ 第1个t秒内、第2个t秒内、……-第n个t秒内的位移之比：
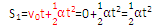               （初速度为0）
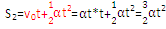           （初速度为at）
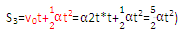        （初速度为2at）

       S_n=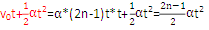   （初速度为）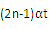
    所以第一个t内、第二个t内、第三个t内……的位移之比为：sⅠ：sⅡ：sⅢ：……：sN=1：3：5：……：(2N-1)；
④前一个s、前两个s、前三个s……所用的时间之比为：
    因为初速度为0，所以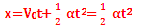
                 
               
             
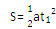
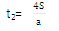
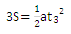
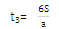
    因此前一个s、前两个s、前三个s……所用的时间之比为：t1：t2：t3：……：tn=1：……：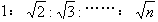
⑤第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ：……：
   
     第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ：……：tN=1：……：      。

      
      

    
     

初速为零的匀变速直线运动中的比例关系（设T为相等的时间间隔，s为相等的位移间隔）：

①T末、2T末、3T末……的瞬时速度之比为：v₁：v₂：v₃：……：v_n=1：2：3：……：n；
②T内、2T内、3T内……的位移之比为：s₁：s₂：s₃：……：s_n=1：4：9：……：n²；
③第一个T内、第二个T内、第三个T内……的位移之比为：s_Ⅰ：s_Ⅱ：s_Ⅲ：……：s_N=1：3：5：……：(2N-1)；
④前一个s、前两个s、前三个s……所用的时间之比为：t₁：t₂：t₃：……：t_n=1：……：；
⑤第一个s、第二个s、第三个s……所用的时间之比为t_Ⅰ、t_Ⅱ、t_Ⅲ：……：t_N=1：……：。

从运动情况确定受力：

1、知道物体的运动情况，应用运动学公式求出物体的加速度，再应用牛顿第二定律，推断或者求出物体的受力情况。
2、分析这类问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、求解动力学这两类问题的思路，可由下面的框图来表示。

瞬时加速度问题的解决方法：

分析物体在某一时刻的瞬时加速度，关键是分析瞬时前后的受力情况及运动状态，再由牛顿第二定律求出瞬时加速度。此类问题应注意以下两种基本模型。
(1)刚性绳(或接触面)：可认为是一种不发生明显形变就能产生弹力的物体。若剪断(或脱离)后，其弹力立即消失，不需要考虑形变恢复时间。一般题目中所给的细绳(线)和接触面，在不加特殊说明时，均可按此模型处理。解决此模型的关键在于分析情景突变后的过程，利用过程的初状态分析求解状态突变后的瞬时加速度。
(2)弹簧(或橡皮绳)：此类物体的特点是形变量大，形变恢复需要较长时间。在瞬时问题中，其弹力的大小往往可以看成不变。但当弹簧的一端不与有质量的物体连接时，轻弹簧的形变不需要时间，弹力可以突变。解决此类问题时需利用情景突变前的受力来确定情景突变后瞬间的受力及加速度。

动力学范围的整体法与隔离法：

处理连接体问题的方法有整体法和隔离法。
1．整体法将一组连接体作为一个整体看待，牛顿第二定律中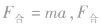是整体受的合外力，只分析整体所受的外力即可(因为连接体的相互作用力是内力，可不分析)，简化了受力分析。在研究连接体时，连接体各部分的运动状态可以相同，也可以不同。当连接体各部分运动状态不同时，整体的合外力等于各部分质量与各部分加速度乘积的矢量和，即F_合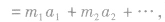写成分量形式有：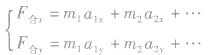

如果待求的问题不涉及系统内部的相互作用时，就可以采用整体法。
2．隔离法在求解连接体的相互作用力时采用，将某个部分从连接体中分离出来，其他部分对它的作用力就成了外力。
整体法与隔离法在研究连接体问题时经常交替使用。