返回

高中二年级物理

首页
首页 高中二年级物理知识 焦耳定律，电热 正弦式交变电流 试题正文
  • 计算题
    如图所示，矩形线圈abcd在磁感强度B=2T的匀强磁场中绕轴OO′，以角速度ω=10πrad／s匀速转动，线圈匝数N=10，总电阻为r=1Ω。ab=0.2m，bc=0.3m，负载电阻R=14Ω。求：
    （1）电阻R在0.2s内所发出的热量；
    （2）0.05s内流过电阻R的电量（设线圈从图示位置开始计时）；
    （3）伏特表的示数；
    （4）框转到图示位置时穿过闭合回路磁通量的变化率。

    本题信息：2011年0117期中题物理计算题难度极难 来源:马凤霞
  • 本题答案
    查看答案
本试题 “如图所示，矩形线圈abcd在磁感强度B=2T的匀强磁场中绕轴OO′，以角速度ω=10πrad／s匀速转动，线圈匝数N=10，总电阻为r=1Ω。ab=0.2m，bc=0.3m，负载电阻R=14Ω。...” 主要考查您对

焦耳定律，电热

正弦式交变电流

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 焦耳定律，电热
  • 正弦式交变电流

电热（焦耳定律）：

1、定义：电流通过电阻为R的导体时，t时间内导体上产生的热量，即电热
2、公式：Q=I2Rt
3、单位：J，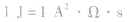
4、物理意义：电流通过导体时所产生的电热
5、适用条件：任何电路
6、能量转化情况：有多少电能转化为热能


电功和电热的关系：
①纯电阻电路消耗的电能全部转化为热能，电功和电热是相等的，所以有W=Q，UIt=I2Rt，U=IR（欧姆定律成立），；
②非纯电阻电路消耗的电能一部分转化为热能，另一部分转化为其他形式的能。所以有W>Q，UIt>I2Rt，U>IR（欧姆定律不成立）。

电功、电热的计算方法:

对任何电路，电流做功均为电流产生的热量均为。
在纯电阻电路中，电功全部转化为电热，能量转化示意图表示为：。则有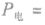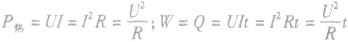，故在计算电功或电热时，可根据题目中的条件，灵活选用以上公式分析计算。
若电流通过非纯电阻电路(如电动机、电解槽等) 时，能量转化的示意图表示为：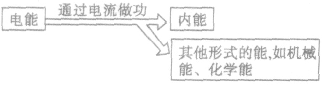
 
1)在非纯电阻电路中，如含有电动机的电路中电能转化为内能和机械能，即；在含有电解槽的电路中电能转化为内能和化学能，即。在这种情况下，电功只能用计算，电热只能用计算。
(2)含有直流电动机的电路不能简单地理解成它一定是一个非纯电阻电路，要从纯电阻电路和非纯电阻电路在能量转化上加以区分。直流电动机两端加上电压以后，若电动机转动，则有电能转化为机械能，此时的电路为非纯电阻电路，部分电路的欧姆定律不再适用。若电动机不转，则没有电能转化为机械能，此时损失的电能全部转化为内能，这时的电路是纯电阻电路。因此，分析电路问题时，要重视从能量的角度出发，这样会使思路清晰，解题变顺利。
(3)纯电阻电路中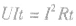，即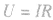；非纯电阻电路中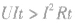，即。


纯电阻电路与非纯电阻电路：



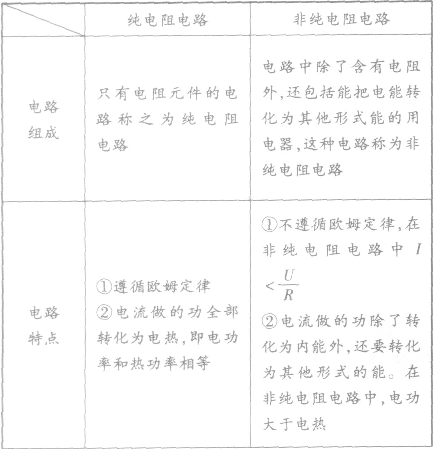
正弦式交变电流：

1．基本产生方法
将闭合线圈置于匀强磁场，并绕垂直于磁场方向的轴做匀速转动，线圈中将产生按正(余)弦规律变化的交流电。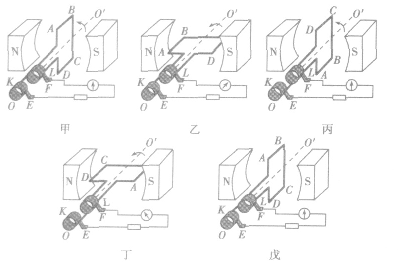

如图所示表示了线圈ABCD在磁场中逆时针转动一周的情况。前半周(甲→乙→丙)电流沿着DCBA方向流动(由右手定则分别判断ABCD边切割磁感线，而AD、BC边不切割磁感线)，后半周(丙→丁→戊)电流方向为ABCD，两种情况交替出现，形成交变电流。
2．正弦式交变电流的其他产生方法
(1)从磁通量角度来看，当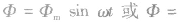时，感应电动势所产生的电流为正弦式交变电流。
①磁场随时间按正弦或余弦规律变化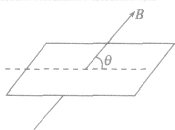

如图所示，当n匝线圈与磁场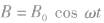成角放置时，设线圈面积为S，线圈中产生的感应电动势为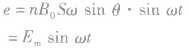
 
②面积随时间按正弦或余弦规律变化
这种情况通常是因导体运动引起的。
③面与磁场夹角随时问均匀变化这是上述产生正弦式交变电流的基本方法。
(2)从导体切割的角度来看，当时，可能的原因由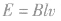可知，可能是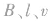中之一随时间变化引起的。
①导体棒运动
如图所示，当导体棒运动的速度满足时，产生的是正弦式交变电流

 
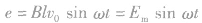
②有效长度变化如图所示，两条相间绝缘的导轨形状满足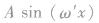，当导体杆MN以速度v匀速沿导轨滑动时，在导轨间导体杆产生的电动势为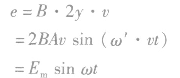


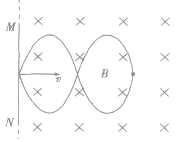
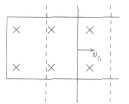
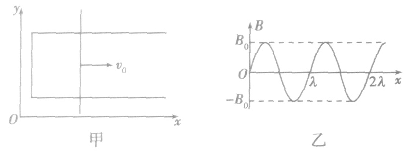
③磁场随空间变化
如图甲所示，磁场垂直于xoy平面，大小只在沿x 轴方向按图乙所示规律发生变化。当导体杆以速度v0 沿x轴匀速运动时，杆产生的是正弦式交变电流。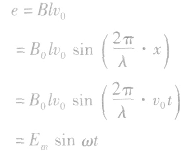



发现相似题
与“如图所示，矩形线圈abcd在磁感强度B=2T的匀强磁场中绕轴OO′，...”考查相似的试题有：