本试题 “下列说法正确的是( )A.由公式E=Fq可知:电场强度E与电场力F成正比,与试探电荷q成反比B.由公式E=kQr2可知:在无限接近带电体处,其电场强度趋于无穷大C....” 主要考查您对电场强度的定义式
点电荷的电场强度
电势差与电场强度的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 电场强度的定义式
- 点电荷的电场强度
- 电势差与电场强度的关系
电场强度:


计算场强的四种方法:
1.计算电场强度的常用方法——公式法
(1)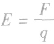 是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
(2)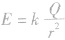 要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
(3)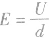 是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
2.计算多个电荷形成的电场强度的方法——叠加法
当空间的电场由几个点电荷共同激发的时候,空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和,其合成遵循矢量合成的平行四边形定则。
3.计算特殊带电体产生的电场强度的方法
(1)补偿法对于某些物理问题,当直接去解待求的A很困难或没有条件求解时,可设法补上一个B,补偿的原则是使A+B成为一个完整的模型,从而使A+B变得易于求解,而且,补上去的B也必须容易求解。这样,待求的A便可从两者的差值中获得,问题就迎刃而解了,这就是解物理题时常用的补偿法。用这个方法可算出一些特殊的带电体所产生的电场强度。
(2)微元法在某些问题中,场源带电体的形状特殊,不能直接求解场源带电体在空间某点所产生的总电场,此时可将场源带电体分割,在高中阶段,这类问题中分割后的微元常有部分微元关于待求点对称,这就可以利用场的叠加及对称性来解题。
4.计算感应电荷产生的电场强度的常用方法—— 静电平衡法根据静电平衡时导体内部场强处处为零的特点,外部场强与感应电荷产生的场强(附加电场)的合场强为零,可知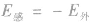 ,这样就可以把复杂问题变简单了。
,这样就可以把复杂问题变简单了。
点电荷的场强:
1、大小:点电荷产生的电场,某点场强大小与场源电荷的电荷量成正比,与该点到场源电荷的距离的平方成反比
2、方向:场源电荷是正电荷时,某点场强方向沿该点与场源电荷的连线背离场源电荷,场源电荷是负电荷时则相反,如图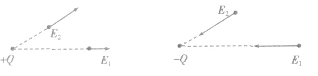
3、表达式:其中Q是场源电荷的电荷量,r是该点到场源电荷的距离
4、适用条件:①真空中②点电荷
场强与电势差的关系:
(1)大小关系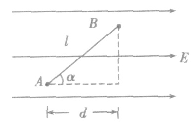
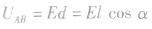 或
或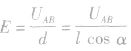 ,公式
,公式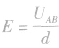 表明,匀强电场的电场强度在数值上等于沿电场强度方向上单位距离的电势差,正是依据这个关系,规定电场强度的单位是V/m。
表明,匀强电场的电场强度在数值上等于沿电场强度方向上单位距离的电势差,正是依据这个关系,规定电场强度的单位是V/m。
(2)适用条件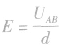 只能用在匀强电场中进行定量计算,在非匀强电场中,E是电势差随空间的变化率,用
只能用在匀强电场中进行定量计算,在非匀强电场中,E是电势差随空间的变化率,用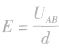 得到的是AB间场强的平均值。
得到的是AB间场强的平均值。
(3)方向关系场强的方向就是电势降低最快的方向。只有沿场强方向,在单位长度上的电势差最大,也就是说电势降低最快的方向为电场强度的方向。但是,电势降低的方向不一定是电场强度的方向。
(4)匀强电场中的三个推论
①匀强电场中相互平行的直线上(包括同一直线) 距离相等的点电势差相同。
②匀强电场中相互平行的直线上,若A、B两点间距离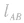 是C、D两点间距离
是C、D两点间距离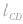 的n倍,则A、B两点间电势差
的n倍,则A、B两点间电势差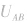 是C、D两点间电势差的n倍,即当
是C、D两点间电势差的n倍,即当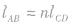 时,
时,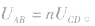
③在匀强电场中同一直线上,若B是A、C的中点,则B点电势等于A、C两点电势的算术平均值,即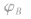
与“下列说法正确的是( )A.由公式E=Fq可知:电场强度E与电场力...”考查相似的试题有:
- 等量异种点电荷的连线和其中垂线如图,现将一个带负点的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点,则检验电...
- 如图所示,A、B均为半个绝缘正方体,质量均为m,在A、B内部各嵌入一个带电小球,A带电量为+q,B带电量为-q,且两个小球的球...
- 四种电场的电场线如图所示.一电荷q仅在电场力作用下由M点向N点作加速运动,且加速度越来越大.则该电荷所在的电场可能是图中...
- 某电场的电场线分布如图所示,关于电场中A、B两点的场强,下列说法正确的是A. =B. <C. >D.点与点的电场强度方向相同
- 下列说法中,正确的是( )A.公式E=Fq只适用于真空中点电荷产生的电场B.由公式U=Wq,说明两点间的电势差U与电场力做功W成正...
- 两个等量异种电荷的连线的垂直平分线上有A、B、C三点,如图所示,下列说法正确的是( )A.a点电势比b点高B.a、b两点的场强...
- 如图所示,水平向右的匀强电场中有直角三角形ABC,∠A=90°,∠B=30°,现在A、B两点分别固定有电荷量绝对值为QA和QB的点电荷,...
- 如图所示,将平行板电容器极板竖直放置,两板间距离d=0.1m,电势差U=1000V,一个质量m=0.2g,带正电q=10-7C的小球(球大小可...
- 一长为L的细线,上端固定,下端拴一质量为m、带电荷量为+q的小球,处于如图所示的水平向右的匀强电场中.开始时,将细线与小...
- 如图所示,在xOy平面内有一个以O为圆心、半径R=0.1m的圆,P为圆周上的一点,O、P两点连线与x轴正方向的夹角为θ.若空间存在沿...