本试题 “小红利用休息时间向爸爸请教一些有关汽车的知识,并作了记录,内容如下表所示,请你根据小红的记录,提出问题,并进行解答.(说明:提出的问题应该是不同方...” 主要考查您对密度公式的应用
速度的计算
惯性现象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 密度公式的应用
- 速度的计算
- 惯性现象
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比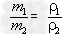 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比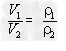 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
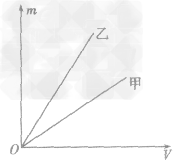
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
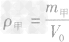 ,ρ乙=
,ρ乙= 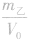 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。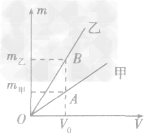
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,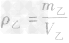
(2)写出该物理量比的表达式:
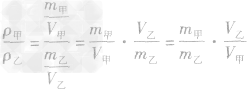
(3)化简:代入已知比值的求解:
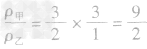
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
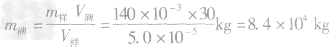 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
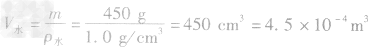 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为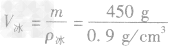 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,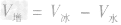 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
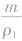 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=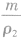 ,合金的体积
,合金的体积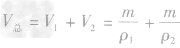 ,则合金的密度
,则合金的密度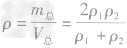
在(2)中两种金属的体积相等,设为
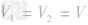 ,合金的体积
,合金的体积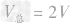 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=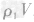 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为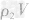 ,合金的质量m总
,合金的质量m总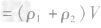 ,合金的密度为
,合金的密度为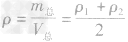 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
计算公式:
v= 。其中v表示速度,s表示路程,t表示通过这段路程所用的时间。
。其中v表示速度,s表示路程,t表示通过这段路程所用的时间。
巧选参照物简化速度的计算:
恰当地选择参照物,可使某些关于速度计算的复杂问题变得简单。像超车、错车,漂流物问题等都可以这样试试!不要形成定势,只盯着地面或地面上静止的物体做参照物!
例1在一列以18m/s的速度匀速行驶的火车上,某乘客以2m/s的速度在车厢内行走(车厢长 20m).下列说法正确的是( )
A.乘客用ls的时间从车厢头走到车厢尾
B.乘客用11s的时间从车厢头走到车厢尾
C.乘客用10s的时间从车厢头走到车厢尾
D,乘客用1.25s的时间从车厢头走到车厢尾
解析研究地面上运动的物体我们首先想到的参照物是地面。本题如果以地面为参照物,火车和乘客都在运动,问题很复杂,如果我们选取匀速行驶的火车为参照物,问题就会简单许多,只剩下一个相对于参照物运动的物体——乘客,无论乘客从车头走到车尾,或从车尾走到车头,相对车厢走的路程都是车厢长 20m,相对于车的速度为2m/s,由速度公式的变形,可求出时间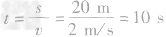 ,则乘客无论从车头走到 车尾或从车尾走到车头所需时间均相等,故正确答案为C。
,则乘客无论从车头走到 车尾或从车尾走到车头所需时间均相等,故正确答案为C。
答案:C
比值类问题解决方法:
求比值的问题,把所给条件写成比的形式后,根据速度公式或者其变形公式,把所要求的硅用比值表示出来,化简,代入数据,计算得出结果。
例甲乙两匀速直线运动的物体的速度之比勾 4:3,运动的时间之比为4:1,则两车通过的路程之比为 ( )
A.4:3
B.4:l
C. 3:4
D.16:3
解析:有速度公式 变形得s=vt,利用速度公式来求路程之比
变形得s=vt,利用速度公式来求路程之比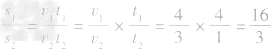 。
。
答案:D
我们把物体保持运动状态不变的特性叫做惯性,惯性是物体的固有属性.
辨析与区别:
惯性”与“第一定律”的区别
“惯性”与“惯性定律”不是同一概念,不能混为一谈。它们的区别:惯性是一切物体固有的属性,是不依外界(作用力)条件而改变,它始终伴随物体而存在。牛顿第一定律则是研究物体在不受外力作用时如何运动的问题,是一条运动定律,它指出了“物体保持匀速直线运动状态或静止状态”的原因。而惯性是“物体具有保持原来的匀速直线运动状态或静止状态”的特性;两者完全不同。为何牛顿第一定律又叫惯性定律,是因为定律中所描述的现象是物体的惯性的一个方面的表现,当物体受到外力作用(合外力不为零)时,物体不可能保持匀速直线运动状态或静止状态,但物体力图保持原有运动状态不变的性质(惯性)仍旧表现出来。
“惯性”与“力”的区别
“惯性”与“力”不是同一概念,“子弹离开枪口后还会继续向前运动”,“水平道路上运动着的汽车关闭发动机后还要向前运动”这些都是惯性。惯性与力的区别:①物理意义不同;惯性是指物体具有保持静止状态或匀速直线运动状态的性质;而力是指物体对物体的作用。惯性是物体本身的属性,始终具有这种性质,它与外界条件无关;力则只有物体与物体发生相互作用时才有,离开了物体就无所谓力。②构成的要素不同:惯性只有大小,没有方向和作用点,而大小也没有具体数值,无单位;力是由大小,方向和作用点三要素构成,它的大小有具体的数值,单位是牛。③惯性是保持物体运动状态不变的性质;力作用则是改变物体的运动状态。④惯性的大小只与物体的质量有关,而力的大小跟许多因素有关(视力的种类而定)。
“物体惯性”与“外力作用”的辨证关系
物体的惯性和外力作用这一对矛盾的对立统一,形成了宏观物体的形形色色的各种复杂的运动。如果没有外力,物体也就没有复杂多样的运动形式;如果没有惯性,物体的运动状态改变不需要力的作用。只有当我们理解了惯性与外力作用的辨证关系,就不难解释惯性现象。例如“锤子松了,把锤把的一端在物体上撞几下,锤头就能紧套在锤柄上”这是因为锤与柄原来都向下运动,柄撞在物体上受到阻力作用,改变了它的运动状态,就停止了运动,锤头没受阻力仍保持原来运动状态,继续向下运动,这样锤头就紧套在锤柄上了。
“惯性”与“速度”的区别
惯性大小与物体运动的快慢无关。“汽车行驶越快,其惯性越大”是不正确的。运动快的汽车难刹车是因为运动速度越快,物体的运动状态越难改变。可见惯性大小与运动状态并无关系。惯性大小只与物体质量有关。
惯性维护平衡与作用造成变化的辩证关系
时效波先生在二十世纪末期论述“生命的产生”时,提出了惯性维护平衡与作用造成变化的辩证关系:“物质是运动的,运动的物质有保持其原有平衡状态(干扰前状态)的属性,即惯性。这里提到的惯性是广义质能意义上的概念,不仅指宏观物体,构成宏观物体、维系着微观结构形态运动着的分子、原子、电子同样具有惯性。物质是运动的,运动的物质之间是相互联系、相互作用的。物质在相互作用的过程中,会发生物质和能量的运动转化,原有的平衡状态(宏观的运动状态、微观的结构形态)就会被改变或打破,形成具有新的运动状态和结构形态的物质。运动的物质有保持原有平衡状态的属性,而运动物质间的相互作用又时刻破坏着平衡,惯性维护平衡与作用造成变化成了物质最基本属性的矛盾统一体。无机物在物质间的相互作用中,只能被动地接受宏观的、微观的冲击和破坏,改变其原有的运动状态和结构形态。如被海水冲刷和风吹日晒的礁石会移动位置和逐渐破碎。原始生命则能为维护自身的平衡状态作出反应,主动地吸收利用物质能量(新陈代谢)来维护有机体的结构形态不受破坏,以维持其原有性能,获得生存。事实上,由碳水化合物构成的蛋白质分子就已经能有选择地从外界吸收营养物并排出分解物,不断与环境中的某些物质进行代谢。”
对惯性的正确认识:
(1)惯性与物体所处的运动状态无关。对任何物体,无论是运动还是静止,无论是运动状态改变还是不变,物体都具有惯性。不能认为:运动的物体具有惯性,静止的物体不具有惯性或物体运动的速度大,惯性就大
(2)惯性大小只与物体的质量有有关。物体的质量越大,其运动状态越难改变,我们就说它的惯性越大;物体的质量越小,其运动状态越容易改变,我们就说它的惯性越小。物理学中就用质量来量度物体惯性的大小
(3)惯性不是力。力是物体对物体的作用,发生力的作用时,必然要涉及两个相互作用的物体,单独一个物体不会产生力的作用;每个物体都具有惯性.不需要两个物体的相互作用,惯性只有大小没有方向,因此不能把惯性说成是“惯性力”“受到惯性作用”或“克服物体的惯性”,一般只能说“具有惯性”
利用惯性鉴别生、熟鸡蛋:
例:小刚同学把一只熟鸡蛋和一只生鸡蛋都放在水平桌面上,用同样大小的力分别使它们在桌面上绕竖直轴水平旋转,然后用手按住熟鸡蛋立即释放,发现熟鸡蛋静止了;用手按住生鸡蛋立即释放,发现生鸡蛋沿原来方向继续转了几圈,如图所示。请用初中物理知识解释为什么释放后生鸡蛋又继续转了几圈?
解析:具体分析过程如下:
(1)确定研究对象及其原来所处状态:本题的研究对象是熟鸡蛋和生鸡蛋,他们都在桌面上绕竖直轴水平旋转。
(2)确定物体的哪部分受力改变运动状态:熟鸡蛋是一个整体,用手按住后整体停止运动;生鸡蛋的蛋壳与蛋清、蛋黄是分离的,用手按住后只是蛋壳停止转动。
(3)确定物体哪部分由于惯性仍保持原来的运动状态:对于熟鸡蛋来说,受力后整体停止运动;对于生鸡蛋来说,壳内的蛋清和蛋黄由于惯性仍会保持原来的运动状态。
(4)造成的结果:手离开鸡蛋后,熟鸡蛋停止转动,生鸡蛋仍继续转动几圈。
答案:这是因为熟鸡蛋蛋壳内的物质变成周体与鸡蛋壳连在一起,用手按住立即静止,而生鸡蛋的蛋黄与蛋壳间有蛋清,用手按住转动的生鸡蛋,蛋内的蛋黄由于惯性还要继续转动,所以手松开后,整个生鸡蛋又继续转几圈。
与“小红利用休息时间向爸爸请教一些有关汽车的知识,并作了记录...”考查相似的试题有:
- 三个质量和体积都相等的铜、铁、铝球,其中一定是空心球的是______;可能空心的是______;若空心注满水质量最大的是______.
- 有一质量为120g的圆柱体空玻璃瓶,按如图所示方式放置在表面积为0.1m2的水平桌面上,瓶子的底面积为0.15×10-3m2,当瓶内装满...
- 有一个玻璃瓶质量为300g,装满水时总质量为800g,装满另一种液体时总质量为700g,求:(1)这个瓶的容积是多少L?(2)另一种...
- 有一串项链质量是30g,把它浸没在盛水的量筒中时,量筒的示数增加了2ml,此项链的密度是______kg/m3.若用纯金制成这样一串项...
- 两根长度和材料都相同的金属导线,若甲导线质量是乙导线质量的3倍,则电阻小的是______导线.
- 如图所示,有一长方体游泳池,长25m,宽12m,水深2m.(池底是水平的) (ρ水=1.0×103kg/m3)(1)求游泳池中水的质量;(2)...
- 人体的密度与水的密度差不多,一个正常的成年人质量约70__________,其体积约为__________m3.
- 冰的密度是0.9×103kg/m3,一杯水结成冰后,体积将______质量将______(填“增大”“减小”或“不变”)
- 小平在高处用望远镜眺望,他看到了远处有一位铁匠在工作.若铁匠以每秒一次的快慢节奏锻打铁块,在他看到铁匠最后一次锻打铁...
- 李钢驾驶一辆摩托车在与铁路平行的公路上以8m/s 的速度匀速直线行驶,铁路上迎面开来一列匀速行驶的火车,已知火车全 长240 m...