本试题 “一名宇航员抵达一半径为R的星球表面后,为了测定该星球的质量,做了如下实验:将一个小球从该星球表面某位置以初速度v竖直向上抛出,小球在空中运动一段时间...” 主要考查您对竖直上抛运动
计算天体质量与密度
人造地球卫星
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 竖直上抛运动
- 计算天体质量与密度
- 人造地球卫星
竖直上抛运动:
将物体以一定初速度沿竖直方向向上抛出,物体只在重力作用下运动(不考虑空气阻力作用),叫做竖直上抛运动。
竖直上抛运动的公式:
vt=v0-gt;h=v0t-![]() gt2;速度位移公式:vt2-v02=-2gh。
gt2;速度位移公式:vt2-v02=-2gh。
运动特征:
①运动到最高点v=0,a=-g(取竖直向下方向为正方向);
②能上升的最大高度hmax=![]() ;
;
③质点在通过同一高度位置时,上升速度与下落速度大小相等;物体在通过一段高度过程中,上升时间与下落时间相等,![]() 。
。
④物体只受重力作用,具有竖直向上的初速度。
运动性质:
初速度不为零的匀变速直线运动。
竖直上抛的处理方法:
1、分段处理法:
①上升阶段:已知v0,a=-g,vt=0的匀减速直线运动,取向上为正方向较方便。所以运动规律为
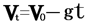 ,
, ,
,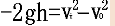
故,上升时间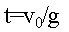 ,最大高度
,最大高度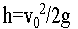 。
。
②最高点v=0,可是不处于静止状态,因为a=g。
③下降阶段:自由落体运动,取向下为正方向较方便。
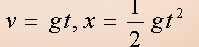
2、对称性:
①竖直上抛的物体上抛达到最大高度与从这一高度落回抛出点所用的时间相等。
②竖直上抛物体在上升和下落过程中经过同一位置时的速度大小相等方向相反。
3、V-t图像:
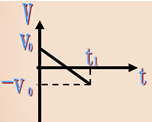
4、整体分析法:
将全过程看成是加速度为-g的匀变速直线运动,应用公式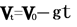 ,
,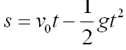
(1)s为正,表示质点在抛出点的上方,s为负表示在抛出点的下方。
(2)由同一s求出的t、可能有两个解,要注意分清其意义。
(3)算出的vt>0表示物体在向上过程中,vt<0表示物体在向下过程中;s>0表示物体在抛出点上方,s<0表示物体在抛出点下方.
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。以地球的质量的计算为例
①若已知月球绕地球做匀速圆周运动的周期T和半径r,根据: 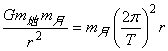 ,得:
,得:![]() ;
;
②若已知月球绕地球做匀速圆周运动的线速度v和半径r,根据: ![]() ,得:
,得:![]() ;
;
③若已知月球绕地球做匀速圆周运动的线速度v和周期T,根据: ![]() 和
和![]() ,得:
,得:![]() ;
;
④若已知地球的半径R和地球表面的重力加速度g,根据: ![]() ,得:
,得:![]() ——此式通常被称为黄金代换式。
——此式通常被称为黄金代换式。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
天体球体积:V=![]() ;天体密度:
;天体密度:![]() (由
(由![]() ,
,![]() ,
,![]() ,r指球体半径,R指轨道半径,当R=r时,
,r指球体半径,R指轨道半径,当R=r时,![]() )。
)。
知识点拨:
科学真是迷人.地球、太阳等天体的质量是多少?天平无法测量.但在我们学习了万有引力定律之后,我们便可以通过它来"称量".求天体质量和密度方法:在地面附近万有引力近似等于物体的重力.由于地球的自转,因而地球表面上的物体随地球自转时需要向心力.所以重力实际上只是万有引力的一个分力,另一个分力就是物体随地球自转时需要的向心力,这个分力与万有引力相比很小忽略不计,可近似认为万有引力等于物体的重力。
人造地球卫星:
在地球上抛出的物体,当它的速度足够大时,物体就永远不会落到地面上,它将围绕地球旋转,成为一颗人造地球卫星,简称人造卫星。
(1)人造卫星按运行轨道可分为低轨道卫星、中轨道卫星、高轨道卫星,以及地球同步轨道卫星、极地轨道卫星等。
(2)按用途人造卫星可分为三大类:科学卫星、技术试验卫星和应用卫星。
人造地球卫星:
1、若已知人造卫星绕地心做匀速率圆周运动的轨道半径为r,地球的质量为M,各物理量与轨道半径的关系:
①由![]() 得卫星运行的向心加速度为:
得卫星运行的向心加速度为:![]() ;
;
②由![]() 得卫星运行的线速度为:
得卫星运行的线速度为:![]() ;
;
③由![]() 得卫星运行的角速度为:
得卫星运行的角速度为: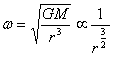 ;
;
④由 得卫星运行的周期为:
得卫星运行的周期为: ;
;
⑤由![]() 得卫星运行的动能:
得卫星运行的动能:![]() ;
;
即随着运行的轨道半径的逐渐增大,向心加速度a、线速度v、角速度ω、动能Ek将逐渐减小,周期T将逐渐增大。
2、用万有引力定律求卫星的高度:
通过观测卫星的周期T和行星表面的重力加速度g及行星的半径R可以求出卫星的高度。
3、近地卫星、赤道上静止不动的物体
①把在地球表面附近环绕地球做匀速率圆周运动的卫星称之为近地卫星,它运行的轨道半径可以认为等于地球的半径R0,其轨道平面通过地心。若已知地球表面的重力加速度为g0,则
由![]() 得:
得:![]() ;
;
由![]() 得:
得: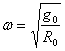 ;
;
由![]() 得:
得: 。
。
若将地球半径R0=6.4×106m和g0=9.8m/s2代入上式,可得v=7.9×103m/s,ω=1.24×10-3rad/s,T=5074s,由于![]() ,
, 和
和 且卫星运行的轨道半径 r>R0,所以所有绕地球做匀速率圆周运动的卫星线速度v<7.9×103m/s,角速度ω<1.24×10-3rad/s,而周期T>5074s。
且卫星运行的轨道半径 r>R0,所以所有绕地球做匀速率圆周运动的卫星线速度v<7.9×103m/s,角速度ω<1.24×10-3rad/s,而周期T>5074s。
②特别需要指出的是,静止在地球表面上的物体,尽管地球对物体的重量也为mg,尽管物体随地球自转也一起转,绕地轴做匀速率圆周运动,且运行周期等于地球自转周期,与近地卫星、同步卫星有相似之处,但它的轨道平面不一定通过地心,如图所示。只有当纬度θ=0°,即物体在赤道上时,轨道平面才能过地心.地球对物体的引力F的一个分力是使物体做匀速率圆周运动所需的向心力f=mω2r,另一个分力才是物体的重量mg,即引力F不等于物体的重量mg,只有当r=0时,即物体在两极处,由于f=mω2r=0,F才等于mg。
③赤道上随地球自转而做圆周运动的物体与近地卫星的区别:
A、赤道上物体受的万有引力只有一小部分充当向心力,另一部分作为重力使得物体紧压地面,而近地卫星的引力全部充当向心力,卫星已脱离地球;
B、赤道上(地球上)的物体与地球保持相对静止,而近地卫星相对于地球而言处于高速旋转状态。
4、卫星的超重和失重
“超重”是卫星进入轨道的加速上升过程和回收时的减速下降过程,此情景与“升降机”中物体超重相同。“失重”是卫星进入轨道后正常运转时,卫星上的物体完全“失重”(因为重力提供向心力),此时,在卫星上的仪器,凡是制造原理与重力有关的均不能正常使用,比如水银气压计、天平、密度计、电子称、摆钟等。
5、卫星变轨问题
卫星由低轨道运动到高轨道,要加速,加速后作离心运动,势能增大,动能减少,到高轨道作圆周运动时速度小于低轨道上的速度。 
当以第一宇宙速度发射人造卫星,它将围绕地球表面做匀速圆周运动;若它发射的速度介于第一宇宙速度与第二宇宙速度之间,则它将围绕地球做椭圆运动。有时为了让卫星绕地球做圆周运动,要在卫星发射后做椭圆运动的过程中二次点火,以达到预定的圆轨道。设第一宇宙速度为v,则由第一宇宙速度的推导过程有![]() 。在地球表面若卫星发射的速度v1>v,则此时卫星受地球的万有引力
。在地球表面若卫星发射的速度v1>v,则此时卫星受地球的万有引力![]() 应小于卫星以v1绕地表做圆周运动所需的向心力m
应小于卫星以v1绕地表做圆周运动所需的向心力m![]() ,故从此时开始卫星将做离心运动,在卫星离地心越来越远的同时,其速率也要不断减小,在其椭圆轨道的远地点处(离地心距离为R′),速率为v2(v2<v1),此时由于G>m
,故从此时开始卫星将做离心运动,在卫星离地心越来越远的同时,其速率也要不断减小,在其椭圆轨道的远地点处(离地心距离为R′),速率为v2(v2<v1),此时由于G>m![]() ,卫星从此时起做向心运动,同时速率增大,从而绕地球沿椭圆轨道做周期性的运动。如果在卫星经过远地点处开动发动机使其速率突然增加到v3,使G=m,则卫星就可以以速率v3,以R′为半径绕地球做匀速圆周运动。同样的道理,在卫星回收时,选择恰当的时机使做圆周运动的卫星速率突然减小,卫星将会沿椭圆轨道做向心运动,让该椭圆与预定回收地点相切或相交,就能成功地回收卫星。
,卫星从此时起做向心运动,同时速率增大,从而绕地球沿椭圆轨道做周期性的运动。如果在卫星经过远地点处开动发动机使其速率突然增加到v3,使G=m,则卫星就可以以速率v3,以R′为半径绕地球做匀速圆周运动。同样的道理,在卫星回收时,选择恰当的时机使做圆周运动的卫星速率突然减小,卫星将会沿椭圆轨道做向心运动,让该椭圆与预定回收地点相切或相交,就能成功地回收卫星。
与“一名宇航员抵达一半径为R的星球表面后,为了测定该星球的质量...”考查相似的试题有:
- 一个热气球以4 m/s2的加速度由静止从地面竖直上升,10 s末从气球上面掉下一重物,此重物最高可上升到距地面多高处?此重物从...
- 质量为0.2kg的物体以24m/s的初速度竖直上抛,由于空气阻力,经2s达到最高点,设物体运动中所受的空气阻力大小不变,g=10m/s2...
- 假如一个做匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍,仍做匀速圆周运动,则[ ]A.根据公式v=ωr,可知卫星的线速...
- 2009年被确定为国际天文年,以纪念伽利略首次用望远镜观测星空400周年.从伽利略的“窥天”创举,到20世纪发射太空望远镜--天文...
- 2005年10月14日5时56分,为确保神舟六号飞船正常运行,在其飞行到第30圈时,在北京航天飞行控制中心的统一指挥调度下,神舟六...
- 2008年9月25日至28日我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱。飞船先沿椭圆轨道飞行,后在远地点343千...
- 已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。⑴推导第一宇宙速度的表达式;⑵若卫星绕地球做匀速圆周运动...
- 2010年1月17日,我国成功发射北斗COMPASS-Gl地球同步卫星.这标志着中国北斗卫星导航系统工程建设又迈出重要一步.关于成功定...
- 光子具有动量,太阳光照射在物体上有压力,慧星的尾巴就是太阳的光压形成的.慧星在绕太阳运转的过程中有时慧尾长,有时慧尾...
- 人造地球卫星绕地球作匀速圆周运动,其轨道半径为R,线速度大小为V。若要使卫星的周期变为2T,下列可行的办法有A.轨道半径R...