本试题 “在建设资源节约型社会里,武汉光谷已经使用风光互补路灯系统(如图所示).风光互补路灯系统具备了风能和太阳能产品的双重优点:没有风能的时候可以通过太阳...” 主要考查您对电功率的计算
密度公式的应用
速度的计算
太阳能
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 电功率的计算
- 密度公式的应用
- 速度的计算
- 太阳能
1. 定义式:P=W/t
2. 常用公式:P=W/t=UIt/t=UI,即P=UI
并、串联电路的总功率:
1.并联电路的总功率
因为P1=I1U,P2=I2U
P=IU=(I1+I2)U=I1U+I2U,所以P=P1+P2
即并联电路的总功率等于各并联用电器的电功率之和。
并联电路电功率的分配:
因为P1=I1U,P2=I2U,
所以
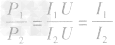
又因为
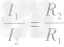 ,所以
,所以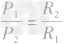
即并联电路中,电功率的分配跟电阻成反比。
2. 串联电路的总功率
因为P1=I1U,P2=I2U
P=IU=(I1+I2)U=I1U+I2U,所以P=P1+P2
即串联电路中总功率等于各串联电器的电功率之和。
串联电路电功率的分配:
因为P1=I1U,P2=I2U
所以
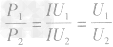
又因为
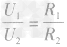 ,所以
,所以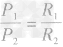
灯泡铭牌问题
“铭牌问题”是电功率知识与实际生活相结合的热点问题,做这类题目时,首先要读懂用电器的“铭牌”。
如图:灯泡上的铭牌。“PZ”是“普通照明灯泡”中 “普”和“照”的汉语拼音的第一个字母,表示灯泡的型号。另外可知:U额=220V,P额=25W。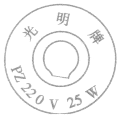
例:甲、乙两灯泡分别标有“220V 40W”和 “110V 40W”字样,将它们串联起来接入220V电路中,比较两灯的亮度,则( )
A.甲灯亮B.乙灯亮 C.一样亮D.无法判断
解析:灯的亮度决定于灯的实际功率,串联时电流相同,根据P=I2R,电阻大的实际功率大,灯更亮一些。根据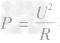 有
有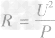 。
。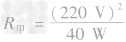 ,R乙=
,R乙= ,所以
,所以 ,甲灯更亮一些。
,甲灯更亮一些。
公式法计算电功率:
1. 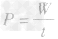
这是电功率的定义式,此公式适用于各种用电器和电路。
2. P=UI
这是电功率的决定式,即电功率是由用电器两端的电压和通过它的电流之积来决定的。此公式适用于所有电路,它是“伏安法”测小灯泡电功率的理论依据。该公式表明,用电器的实际功率等于实际电压与实际电流的乘积。常常借助于用电器的铭牌用此公式来计算用电器的额定电流,进而计算用电器的电阻;当然这个公式的最大用处还是用来计算各类用电器实际消耗的电功率或电路的总功率。
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比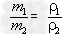 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比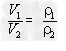 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
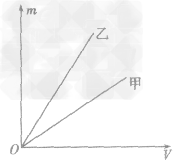
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
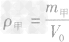 ,ρ乙=
,ρ乙= 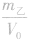 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。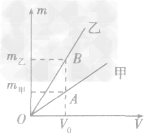
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,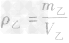
(2)写出该物理量比的表达式:
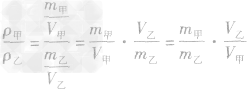
(3)化简:代入已知比值的求解:
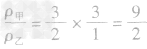
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
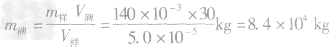 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
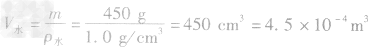 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为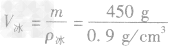 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,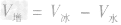 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
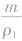 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=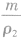 ,合金的体积
,合金的体积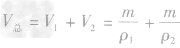 ,则合金的密度
,则合金的密度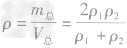
在(2)中两种金属的体积相等,设为
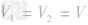 ,合金的体积
,合金的体积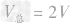 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=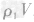 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为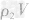 ,合金的质量m总
,合金的质量m总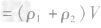 ,合金的密度为
,合金的密度为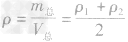 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
计算公式:
v= 。其中v表示速度,s表示路程,t表示通过这段路程所用的时间。
。其中v表示速度,s表示路程,t表示通过这段路程所用的时间。
巧选参照物简化速度的计算:
恰当地选择参照物,可使某些关于速度计算的复杂问题变得简单。像超车、错车,漂流物问题等都可以这样试试!不要形成定势,只盯着地面或地面上静止的物体做参照物!
例1在一列以18m/s的速度匀速行驶的火车上,某乘客以2m/s的速度在车厢内行走(车厢长 20m).下列说法正确的是( )
A.乘客用ls的时间从车厢头走到车厢尾
B.乘客用11s的时间从车厢头走到车厢尾
C.乘客用10s的时间从车厢头走到车厢尾
D,乘客用1.25s的时间从车厢头走到车厢尾
解析研究地面上运动的物体我们首先想到的参照物是地面。本题如果以地面为参照物,火车和乘客都在运动,问题很复杂,如果我们选取匀速行驶的火车为参照物,问题就会简单许多,只剩下一个相对于参照物运动的物体——乘客,无论乘客从车头走到车尾,或从车尾走到车头,相对车厢走的路程都是车厢长 20m,相对于车的速度为2m/s,由速度公式的变形,可求出时间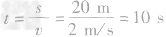 ,则乘客无论从车头走到 车尾或从车尾走到车头所需时间均相等,故正确答案为C。
,则乘客无论从车头走到 车尾或从车尾走到车头所需时间均相等,故正确答案为C。
答案:C
比值类问题解决方法:
求比值的问题,把所给条件写成比的形式后,根据速度公式或者其变形公式,把所要求的硅用比值表示出来,化简,代入数据,计算得出结果。
例甲乙两匀速直线运动的物体的速度之比勾 4:3,运动的时间之比为4:1,则两车通过的路程之比为 ( )
A.4:3
B.4:l
C. 3:4
D.16:3
解析:有速度公式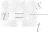 变形得s=vt,利用速度公式来求路程之比
变形得s=vt,利用速度公式来求路程之比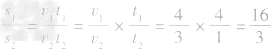 。
。
答案:D
太阳能,一般是指太阳光的辐射能量,在现代一般用作发电。自地球形成生物就主要以太阳提供的热和光生存,而自古人类也懂得以阳光晒干物件,并作为保存食物的方法,如制盐和晒咸鱼等。但在化石燃料减少下,才有意把太阳能进一步发展。太阳能的利用有被动式利用(光热转换)和光电转换两种方式。太阳能发电一种新兴的可再生能源。广义上的太阳能是地球上许多能量的来源,如风能、化学能、水的势能等等。
太阳能的利用及其优、缺点:
| 利用太阳能的三种方式 | 太阳能转化为内能 | 太阳能热水器 |
| 太阳能转化为电能 | 太阳能电池 | |
| 太阳能转化为化学能 | 植物进行光合作用 | |
| 太阳能的优点 | 完全清洁、无污染,并且取之不尽,用之不竭 | |
| 太阳能的缺点 | 太阳能太分散,收集和转换系统过于庞大,因而造价高;随气候、季节变化,不稳定,转换效率低 | |
间接利用太阳能:化石能源(光能→化学能)、生物质能(光能→化学能)
直接利用太阳能:集热器(有平板型集热器、聚光式集热器)(光能→内能),太阳能电池(光能→电能)一般应用在人造卫星、宁宙飞船、打火机、手表等方面。
能源之母——太阳能
太阳主要由最轻的元素——氢构成,其表面的温度高达6000℃,中心的温度高达1500万~2000万摄氏度。数十亿年来,太阳一直不知疲倦地向太空辐射着巨量的光和热。在它内部不停地进行着核聚变反应氧不断地发生核聚变反应,生成氦,同时释放出巨大核能,发出光和热。令人称奇的是,太阳不断地向四面八方的宇宙空间辐射能量,到达地球上的光和热不过是辐射出总能量的22亿分之一,即便如此,地球每秒钟也能接收到173万亿下瓦的能量。这个数字相当于目前全世界能源总消费量的几万倍。现在,太阳光已经照耀我们的地球50亿年了,地球在这50亿年中积累的太阳能是我们所用大部分能量的源泉。地球上的能量除地热能、潮汐能和核能外,绝大多数都是直接或间接地来源于太阳,因此太阳能也被誉为人类的能源之母。
与“在建设资源节约型社会里,武汉光谷已经使用风光互补路灯系统...”考查相似的试题有:
- 各种不同的用电器各不相同,功率为200W的用电器可能是[ ]A、空调B、吸尘器C、电子计算机D、学生计算器
- 两电阻分别标有“4Ω 16W”和“5Ω 20W”,如果把它们并联在同一电路中,则干路中允许的最大电流为( )A.4AB.3.6AC.5AD.2A
- 如图所示是一种产品的LED(发光二极管)手电筒,它由5个LED并联组成,用两节干电池做电源,正常每只LED通过的电流为15mA,则...
- 下列几种估测中,比较符合实际情况的是( )A.教室内天花板离地面的高度约为8mB.60W照明电灯正常工作时的电流是1AC.中学生...
- 太阳能热水器是一种常见的利用太阳能的装置,某品牌太阳能热水器,在晴天能接受到的太阳能的平均辐射强度(用R表示)为R=300J...
- 两个同种材料制成的实心球,甲球是1000g,乙球是200g,它们的质量之比是___________,它们的体积之比是__________,密度之比...
- 高速公路上为避免发生汽车追尾事故,有关部门在公路边竖立了距离确认牌.小明巧妙地利用确认牌估测出了自己乘坐的汽车的速度...
- 下面是一些与一名普通中学生有关的数据,你认为最接近事买的是[ ]A.他的手指甲宽度约为1cmB.他步行的速度约为15m/sC.站立...
- 目前直接利用太阳能的途径有两种:一种是把太阳能转化为 能,如用太阳能热水器加热水;另一种是把太阳能转化为 能,如太阳能...
- 《深圳商报》2004年3月11日报道:近日一种新型太阳能公共卫生间落户北京东郊民巷,该卫生间的能源全部由位于顶部的太阳能电池...