圆锥摆的知识：

圆锥摆模型的结构特点——一根质量和伸长可以不计的线，系一个可以视为质点的摆球，在水平面内做匀速圆周运动，且在摆线沿顶点位置不变的圆锥面上运动。

圆锥摆的特点：

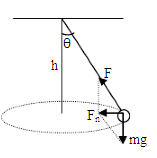
1、圆锥摆模型的受力特点——只受两个力：竖直向下的重力（mg）和沿摆线方向的拉力（F），二力的合力就是摆球做圆周运动的向心力（F_n），如图所示。

2、向心力和向心加速度的计算
设摆球的质量为m，摆长为l，与竖直方向的夹角为θ，摆球的线速度、角速度、周期和频率依次为v、ω、T和f。如图所示，根据不同的条件
向心力可以表示为：；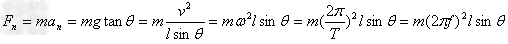
向心加速度可表示为：。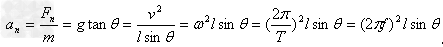
3、摆线拉力的计算计算
摆线的拉力，有两种基本思路：
①当θ角已知时，；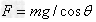
②当θ角未知时，。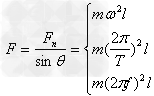
4、周期T、频率f和角速度ω的计算
根据向心加速度公式，有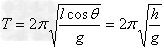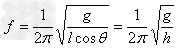，，。式中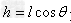为摆球的轨道平面到悬点的距离，即圆锥摆的高度。由这些公式可知，高度相同的圆锥摆，即等高圆锥摆的T、f和ω相等，与m、l和θ无关。
5、漏斗摆：物体在光滑的漏斗形容器内壁的某水平面上做匀速圆周运动。漏斗摆的力学特点：物体只受两个力，竖直向下的重力mg，垂直于漏斗壁的弹力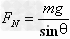，两个力的合力水平指向转轴，其向心力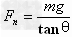。如图所示。

①向心加速度的计算
，θ角一定，故a_n恒定。
②周期T、角速度ω、线速度v的计算（设匀速圆周运动的平面离漏斗尖端距离为h）
由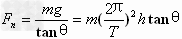，得；
由，得；
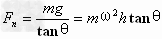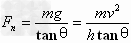由，得。
可见，h增大，线速度增大，角速度减小，周期增大。

结构特点：
一根质量和伸长可以不计的线，系一个可以视为质点的摆球，在水平面内作匀速圆周运动。

受力特点：
只受两个力：竖直向下的重力 mg 和沿摆线方向的拉力 F 。两个力的合力，就是摆球作圆周运动的向心力 F n