本试题 “一个身高为1.68m的中学生站在平面镜前5m远的正前方,当他以1m/s的速度向平面镜靠近时,关于“镜中的像”说法有误的是( )A.2s后像与人之间的距离是6m,像的大...” 主要考查您对平面镜成像的特点和原因
密度公式的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平面镜成像的特点和原因
- 密度公式的应用
平面镜成像的特点:
①像和物体大小相等
②像和物体到镜面的距离相等
③像和物体的连线跟镜面垂直
④物体在平面镜中所成的像是虚像
以上可以缩句为:“物像等大、连线垂直、等距虚像”。
平面镜成像的原理:
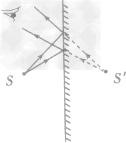
平面镜所成的像是物体发出(或反射)的光线射到镜面上发生反射,由反射光线的反向延长线在镜后相交而形成的,如图所示。点光源s在镜后的像s’并不是实际光线会聚形成的,而是由反射光线的反向延长线相交形成的,所以s’叫做s的虚像。如果把光屏放在s’处,是接收不到这个像的,所以虚像只能用眼睛看到,而不能成在屏上
解释:
照镜子就是这样的原理。可以说,只要利用到平面镜,就一定是反射。 平面镜中的像是由光的反射光线的延长线的交点形成的,所以平面镜中的像是虚像。虚像与物体等大,距离相等。像和物体的大小相等。所以像和物体对镜面来说是对称的。 根据平面镜成像的特点,像和物的大小,总是相等的。无论物体与平面镜的距离如何变化,它在平面镜中所成的像的大小始终不变,与物体的大小总一样。但由于人在观察物体时都有“近大远小”的感觉,当人走向平面镜时,视觉确实觉得像在“变大”,这是由于人眼观察到的物体的大小,不仅仅与物体的真实大小关于,而且还与“视角”密切相关。从人眼向被观察物体的两端各引一条直线,这两条直线的夹角即为“视角”,如果视角大,人就会认为物体大,视角小,人就会认为物体小。当人向平面镜走近时,像与人的距离小了,人观察物体的视角也就增大了,因此所看到的像也就感觉变大了,但实际上像与人的大小始终是相等的,这就是人眼看物体“近大远小”的原因。这正如您看到前方远处向您走来一个人一样,一开始看到是一个小黑影,慢慢变得越来越大,走到您面前时更大,其实那一个小黑影和走到您面前的人是一样大的,只是因为视觉的关系,平面镜成像的像和物关于镜面对称,因此人逐渐靠近镜面。像也一定逐渐靠近镜面,人的感觉是“近大远小”,这是一种视觉效果。
小孔成像及平面镜成像的区别
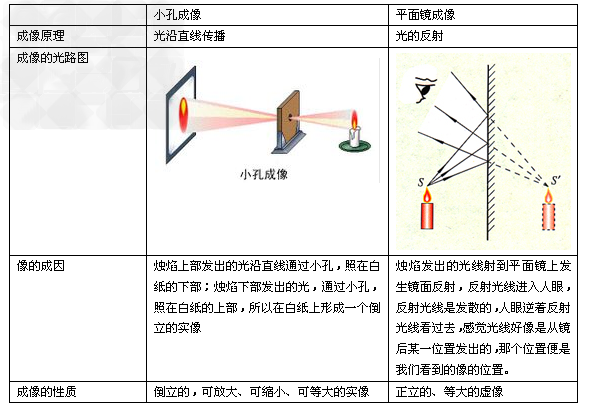
探究平面镜成像的科学方法:
在做平面镜成像的实验中,用玻璃板代替平面镜是因为平面镜成的像是虚像,无法用光屏承接,我们用未点燃的蜡烛去代替像的原因是因为像是虚像,我们没有办法确定它在哪里,用蜡烛与像重合,也就确定了像的大小及位置,我们这样确定像凭的是视觉效果相同,这种方法叫等效替代或等效代换。
有关成像规律的计算
根据平面镜的成像特点可知:像和物关于平面镜是对称的,由于物体到镜面的距离和像到镜面的距离相等,则物体到镜面的距离变化了多少,像到镜面的距离也变化多少。若变化的时间相等,则物体移动的速度和像移动的速度相等,像相对于物体的速度是物体速度的2倍。
例一个人站在镜子前2.5m的地方,则人和像的距离为__m,人向前1m,则人和像之间的距离缩短了__m,此人在镜子中的像的大小将__ (填“变大”、“变小”或“不变”)。
解析 根据平面镜成像的特点,人和像的距离应为2.5×2=5m。人向前1m,像也向前1m,故两者距离缩短2m。像的大小始终与人等大。
答案 5 2 不变
用对称法解决平面镜成像的作图
对称思想作为一种科学研究思想,应用于平面镜解题时,可启发直觉思维,使许多问题不必进行全面周全的论述,借助于对称性即可直接做出判断。
平面镜的成像特点是:像和物的大小相等;它们到平面镜的距离相等;像和物的连线与平面镜垂直。像和物关于平面镜是对称的,这种对称性广泛地应用在了平面镜作图上。如图所示,是关于平面镜成像的几个变式。不管物体如何复杂,平面镜位置如何变化,还是考查角度如何变化,但有一条始终不变,那就是像和物的“对称性”。

例1:请在图中画出物体AB在平面镜中所成的像A’B’。
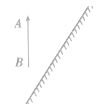
解析:根据平面镜成像特点:像与物大小相等,连线与平面镜垂直,关于平面镜对称,成的像是虚像。分别作A、B相对平面镜的对称点A’、B’,再用虚线连接 A’B’。
答案:如图所示
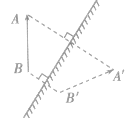
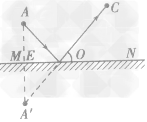
例2:如图所示,物体位于平面镜前方A点,眼睛位于平面镜前方C点。请作出物体发出的光线经平面镜反射后进入眼睛的光路图。

解析:(1)过A点作MN的垂线AE,延长AE至 A',使A'E=AE,A’为物A的像。
(2)连接A'C与MN交于0点,0点为入射点(DC 是反射光线)。
(3)连接AO,并在AO、OC上画出箭头表示光的传播方向,AO就是入射光线,OC是经平面镜反射通过眼睛的光线。
答案:如图所示
巧解平面镜的时钟问题
(1)逆向读法
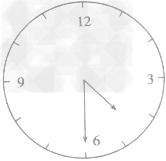
根据平面镜成像规律和成像性质,镜中“钟面”与实际钟面总是相对于平面镜对称。即实际时钟(如图甲所示)的指针按顺时针方向走动时,镜中“钟面”内表示钟点的数字是按上“12”、下“6”、左“3”和右“9”排列。如图乙所示的实际时刻为7:30。
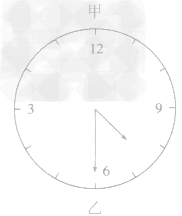
(2)还原法
由平面镜成像的性质,镜叶1“钟面”与实际钟面左右对称。因此,镜中“钟面”的“背面”与实际钟面相对应.即还原出一个实际的钟面。这样,对印刷在书籍或试卷上的镜中“钟面”,只要从其背面对着光亮处透视 “钟面”并直接从中读取钟点数,即为实际钟点数?如图乙所示镜中“钟面”读得实际点数为7:30.
(3)对称作图法根据平面镜成像性质——像与物左右对称。.镜中 “钟面”内的“指针”位置与实际钟面内的指针位置对称。因此,求解这类“镜中时钟”问题,只要由镜中“钟面”作出以上“12”下“6”为对称轴的指针位置图形,再对作出的图形按实际钟面读出钟点数。图所示虚线为实线所示镜中“指针”的左右对称图形,读得实际钟点数为9:40。
等效替代法探究平面镜的成像特点
等效替代法就是在保证某一方面效果相同的前提下,用理想的、熟悉的、简单的物理对象、物理过程、物理现象替代实际的、陌生的、复杂的物理对象、物理过程、物理现象的思想方法。主要有:物理模型的等效替代,物理过程的等效替代,作用效果的等效替代以及物理图形的等效替代等形式例小红同学在做“探究平面镜成像”的实验时,将一块玻璃板竖直放存水平台上,再取两段完全相同的蜡烛。A和B,点燃玻璃板前的蜡烛A,进行观察,如图所示,在此实验中:

(1)小红选择玻璃板代替镜子进行实验的目的是______________。
(2)刻度K的作用是便于比较像与物________________。
__关系。
(3)选取两段完全相同的蜡烛是为了比较像与物的__关系。
(4)移走后面的蜡烛B,并在其所存位置上放一光屏,则光屏上____接收到蜡烛烛焰的像(选填 “能”或“不能”)。所以平面镜所成的像是____ (选填“实”或“虚”)像。
(5)小红将蜡烛A逐渐远离玻璃板时,它的像的大小(选填“变大”、“变小”或“不变”)。
(6)在玻璃板的同一侧,该同学通过玻璃看到了同一个蜡烛的两个像,产生这种现象的原因是_____。
解析:研究平面镜成像特点时,要研究像的大小、倒正及到平面镜的距离关系等,采用玻璃板的目的是利用了玻璃板能透光,在物A侧能观察到另一侧的情况,这样当A的像与另一侧B重合时,说明B所在位置就是A的像的位置,观察像与物的大小关系,并用刻度尺测出A、B分别到平面镜的距离,就可判断两距离大小和像的大小。当取走B,放上光屏时,在光屏上得不到像,而只能用眼睛存物一侧观察玻璃板才能看到,所以说平面镜所成的像是一个正立、等大的虚像,当物体逐渐远离平面镜时,像的大小不变。
答案:(1)能准确找到像的位置 (2)到平面镜的距离 (3)大小 (4)不能 虚 (5)不变 (6)玻璃的两个表面同时发生反射,各成一个像
同一物体靠近或远离平面镜时,像的大小变化问题
物体在平面镜中成的是正立的虚像,像与物体大小相等,即像的大小与物体的大小有关,与物体距平面镜的远近、平面镜的大小等因素无关。
例:某同学从远处走向一面穿衣镜,他住镜中像的大小及像和人之问的距离的变化情况正确的是 ( )
A.像大小不变,像和人之问的距离变小
B.像变大,像和人之间的距离变大
C.像变大,像和人之间的距离变小
D.像大小不变,像和人之间的距离不变
解析:像的大小与物体到平面镜的距离无关,我们平常说的所谓远小近大,只是人的视觉造成的错觉。根据平面镜成像特点可以知道,像和物大小相等,像和物到镜面的距离相等。因为该同学的大小没有变化,所以像大小小变;而该同学到平面镜的距离在变小,所以像到平面镜的距离也在变小,从而像和人之间的距离在变小。
答案:A
①像和物体大小相等
②像和物体到镜面的距离相等
③像和物体的连线跟镜面垂直
④物体在平面镜中所成的像是虚像
以上可以缩句为:“物像等大、连线垂直、等距虚像”。
平面镜成像的原理:
平面镜所成的像是物体发出(或反射)的光线射到镜面上发生反射,由反射光线的反向延长线在镜后相交而形成的,如图所示。点光源s在镜后的像s’并不是实际光线会聚形成的,而是由反射光线的反向延长线相交形成的,所以s’叫做s的虚像。如果把光屏放在s’处,是接收不到这个像的,所以虚像只能用眼睛看到,而不能成在屏上

解释:
照镜子就是这样的原理。可以说,只要利用到平面镜,就一定是反射。 平面镜中的像是由光的反射光线的延长线的交点形成的,所以平面镜中的像是虚像。虚像与物体等大,距离相等。像和物体的大小相等。所以像和物体对镜面来说是对称的。 根据平面镜成像的特点,像和物的大小,总是相等的。无论物体与平面镜的距离如何变化,它在平面镜中所成的像的大小始终不变,与物体的大小总一样。但由于人在观察物体时都有“近大远小”的感觉,当人走向平面镜时,视觉确实觉得像在“变大”,这是由于人眼观察到的物体的大小,不仅仅与物体的真实大小关于,而且还与“视角”密切相关。从人眼向被观察物体的两端各引一条直线,这两条直线的夹角即为“视角”,如果视角大,人就会认为物体大,视角小,人就会认为物体小。当人向平面镜走近时,像与人的距离小了,人观察物体的视角也就增大了,因此所看到的像也就感觉变大了,但实际上像与人的大小始终是相等的,这就是人眼看物体“近大远小”的原因。这正如您看到前方远处向您走来一个人一样,一开始看到是一个小黑影,慢慢变得越来越大,走到您面前时更大,其实那一个小黑影和走到您面前的人是一样大的,只是因为视觉的关系,平面镜成像的像和物关于镜面对称,因此人逐渐靠近镜面。像也一定逐渐靠近镜面,人的感觉是“近大远小”,这是一种视觉效果。
小孔成像及平面镜成像的区别

探究平面镜成像的科学方法:
在做平面镜成像的实验中,用玻璃板代替平面镜是因为平面镜成的像是虚像,无法用光屏承接,我们用未点燃的蜡烛去代替像的原因是因为像是虚像,我们没有办法确定它在哪里,用蜡烛与像重合,也就确定了像的大小及位置,我们这样确定像凭的是视觉效果相同,这种方法叫等效替代或等效代换。
有关成像规律的计算
根据平面镜的成像特点可知:像和物关于平面镜是对称的,由于物体到镜面的距离和像到镜面的距离相等,则物体到镜面的距离变化了多少,像到镜面的距离也变化多少。若变化的时间相等,则物体移动的速度和像移动的速度相等,像相对于物体的速度是物体速度的2倍。
例一个人站在镜子前2.5m的地方,则人和像的距离为__m,人向前1m,则人和像之间的距离缩短了__m,此人在镜子中的像的大小将__ (填“变大”、“变小”或“不变”)。
解析 根据平面镜成像的特点,人和像的距离应为2.5×2=5m。人向前1m,像也向前1m,故两者距离缩短2m。像的大小始终与人等大。
答案 5 2 不变
用对称法解决平面镜成像的作图
对称思想作为一种科学研究思想,应用于平面镜解题时,可启发直觉思维,使许多问题不必进行全面周全的论述,借助于对称性即可直接做出判断。
平面镜的成像特点是:像和物的大小相等;它们到平面镜的距离相等;像和物的连线与平面镜垂直。像和物关于平面镜是对称的,这种对称性广泛地应用在了平面镜作图上。如图所示,是关于平面镜成像的几个变式。不管物体如何复杂,平面镜位置如何变化,还是考查角度如何变化,但有一条始终不变,那就是像和物的“对称性”。

例1:请在图中画出物体AB在平面镜中所成的像A’B’。

解析:根据平面镜成像特点:像与物大小相等,连线与平面镜垂直,关于平面镜对称,成的像是虚像。分别作A、B相对平面镜的对称点A’、B’,再用虚线连接 A’B’。
答案:如图所示

例2:如图所示,物体位于平面镜前方A点,眼睛位于平面镜前方C点。请作出物体发出的光线经平面镜反射后进入眼睛的光路图。

解析:(1)过A点作MN的垂线AE,延长AE至 A',使A'E=AE,A’为物A的像。
(2)连接A'C与MN交于0点,0点为入射点(DC 是反射光线)。
(3)连接AO,并在AO、OC上画出箭头表示光的传播方向,AO就是入射光线,OC是经平面镜反射通过眼睛的光线。
答案:如图所示

巧解平面镜的时钟问题
(1)逆向读法
根据平面镜成像规律和成像性质,镜中“钟面”与实际钟面总是相对于平面镜对称。即实际时钟(如图甲所示)的指针按顺时针方向走动时,镜中“钟面”内表示钟点的数字是按上“12”、下“6”、左“3”和右“9”排列。如图乙所示的实际时刻为7:30。


(2)还原法
由平面镜成像的性质,镜叶1“钟面”与实际钟面左右对称。因此,镜中“钟面”的“背面”与实际钟面相对应.即还原出一个实际的钟面。这样,对印刷在书籍或试卷上的镜中“钟面”,只要从其背面对着光亮处透视 “钟面”并直接从中读取钟点数,即为实际钟点数?如图乙所示镜中“钟面”读得实际点数为7:30.
(3)对称作图法根据平面镜成像性质——像与物左右对称。.镜中 “钟面”内的“指针”位置与实际钟面内的指针位置对称。因此,求解这类“镜中时钟”问题,只要由镜中“钟面”作出以上“12”下“6”为对称轴的指针位置图形,再对作出的图形按实际钟面读出钟点数。图所示虚线为实线所示镜中“指针”的左右对称图形,读得实际钟点数为9:40。
等效替代法探究平面镜的成像特点
等效替代法就是在保证某一方面效果相同的前提下,用理想的、熟悉的、简单的物理对象、物理过程、物理现象替代实际的、陌生的、复杂的物理对象、物理过程、物理现象的思想方法。主要有:物理模型的等效替代,物理过程的等效替代,作用效果的等效替代以及物理图形的等效替代等形式例小红同学在做“探究平面镜成像”的实验时,将一块玻璃板竖直放存水平台上,再取两段完全相同的蜡烛。A和B,点燃玻璃板前的蜡烛A,进行观察,如图所示,在此实验中:

(1)小红选择玻璃板代替镜子进行实验的目的是______________。
(2)刻度K的作用是便于比较像与物________________。
__关系。
(3)选取两段完全相同的蜡烛是为了比较像与物的__关系。
(4)移走后面的蜡烛B,并在其所存位置上放一光屏,则光屏上____接收到蜡烛烛焰的像(选填 “能”或“不能”)。所以平面镜所成的像是____ (选填“实”或“虚”)像。
(5)小红将蜡烛A逐渐远离玻璃板时,它的像的大小(选填“变大”、“变小”或“不变”)。
(6)在玻璃板的同一侧,该同学通过玻璃看到了同一个蜡烛的两个像,产生这种现象的原因是_____。
解析:研究平面镜成像特点时,要研究像的大小、倒正及到平面镜的距离关系等,采用玻璃板的目的是利用了玻璃板能透光,在物A侧能观察到另一侧的情况,这样当A的像与另一侧B重合时,说明B所在位置就是A的像的位置,观察像与物的大小关系,并用刻度尺测出A、B分别到平面镜的距离,就可判断两距离大小和像的大小。当取走B,放上光屏时,在光屏上得不到像,而只能用眼睛存物一侧观察玻璃板才能看到,所以说平面镜所成的像是一个正立、等大的虚像,当物体逐渐远离平面镜时,像的大小不变。
答案:(1)能准确找到像的位置 (2)到平面镜的距离 (3)大小 (4)不能 虚 (5)不变 (6)玻璃的两个表面同时发生反射,各成一个像
同一物体靠近或远离平面镜时,像的大小变化问题
物体在平面镜中成的是正立的虚像,像与物体大小相等,即像的大小与物体的大小有关,与物体距平面镜的远近、平面镜的大小等因素无关。
例:某同学从远处走向一面穿衣镜,他住镜中像的大小及像和人之问的距离的变化情况正确的是 ( )
A.像大小不变,像和人之问的距离变小
B.像变大,像和人之间的距离变大
C.像变大,像和人之间的距离变小
D.像大小不变,像和人之间的距离不变
解析:像的大小与物体到平面镜的距离无关,我们平常说的所谓远小近大,只是人的视觉造成的错觉。根据平面镜成像特点可以知道,像和物大小相等,像和物到镜面的距离相等。因为该同学的大小没有变化,所以像大小小变;而该同学到平面镜的距离在变小,所以像到平面镜的距离也在变小,从而像和人之间的距离在变小。
答案:A
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比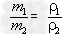 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比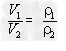 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
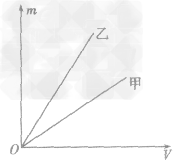
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
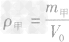 ,ρ乙=
,ρ乙= 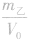 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。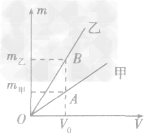
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,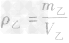
(2)写出该物理量比的表达式:
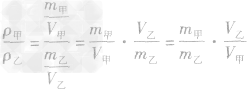
(3)化简:代入已知比值的求解:
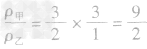
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
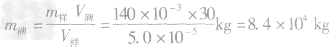 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
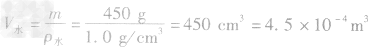 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为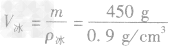 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,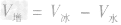 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
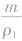 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=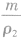 ,合金的体积
,合金的体积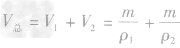 ,则合金的密度
,则合金的密度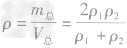
在(2)中两种金属的体积相等,设为
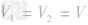 ,合金的体积
,合金的体积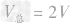 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=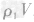 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为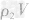 ,合金的质量m总
,合金的质量m总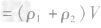 ,合金的密度为
,合金的密度为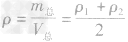 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
发现相似题
与“一个身高为1.68m的中学生站在平面镜前5m远的正前方,当他以1m...”考查相似的试题有:
- 一常用温度计(此时银白色液柱长8cm)逐渐向平面镜靠近,在靠近的过程中,在镜中所成像长度 __(填“变大”“变小”或“不变”).若...
- 渔民叉鱼时,看到的鱼是 ______像,这是因为光在水面处发生 ______的缘故.人在平静的河水里看到水中的云,这是由于光的 ____...
- 如图所示,蜡烛在平面镜M中所成像的位置应在图中的[ ]A、甲处B、乙处C、丙处D、丁处
- 某瓶中装满水时,称其质量为88g.若再装入10g砂粒,水溢出后,把瓶外部的水擦干,称其质量为94g,则沙粒的密度为______kg/m3.
- 下列说法正确的是( )A.吸油烟机能将油烟吸走,是利用空气流动越快,压强越大的原理B.给病人测体温时体温计中水银在温度上...
- 5kg的水结成冰后质量是______kg,体积______(“增大”、“不变”、“减小”),密度______(“增大”、“不变”、“减小”).
- 质量相等的铜块和铁块,铜块的体积______,铁块的体积______.(填“大”或“小”)
- 物理上常把电流的形成与水流的形成进行类比。阅读以下材料,完成填空和推导。(1 )水管中的水朝一定方向流动,就会形成水流...
- 图是在探究甲、乙两种物质质量跟体积关系时作出的图象.以下分析正确的是( ) A.不同物质的质量跟体积的比值是不同的 B.甲...
- 一边长为0.1m,质量为4.45kg的正方形铜块,平放在水平桌面上, 求:(1)铜块该对水平桌面的压强;(2)通过计算说明铜块是空...