本试题 “如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则由此( )A.可求M、N之间的距离B.可求小球落到N点时速...” 主要考查您对平抛运动
功
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平抛运动
- 功
平抛运动的定义:
将物体以一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动,叫做平抛运动。
平抛运动的特性:
以抛出点为坐标原点,水平初速度V0,竖直向下的方向为y轴正方向,建立如图所示的坐标系,在该坐标系下,对任一时刻t: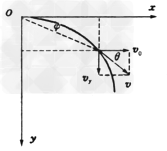
①位移
分位移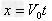 (水平方向),
(水平方向),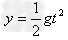 (竖直方向);
(竖直方向);
合位移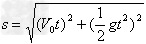 ,
, (φ为合位移与x轴夹角)。
(φ为合位移与x轴夹角)。
②速度
分速度 (水平方向),Vy=gt(竖直方向);
(水平方向),Vy=gt(竖直方向);
合速度 ,
,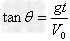 (θ为合速度V与x轴夹角)。
(θ为合速度V与x轴夹角)。
③平抛运动时间: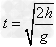 (取决于竖直下落的高度)。
(取决于竖直下落的高度)。
④水平射程: (取决于竖直下落的高度和初速度)。
(取决于竖直下落的高度和初速度)。
类平抛运动:
(1)定义当物体所受的合外力恒定且与初速度垂直时,物体做类平抛运动。
(2)类平抛运动的分解方法
①常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性。
②特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为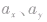 ,,初速度
,,初速度 分解为
分解为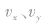 ,然后分别在x、y方向上列方程求解。
,然后分别在x、y方向上列方程求解。
(3)类平抛运动问题的求解思路
根据物体受力特点和运动特点判断该问题属于类平抛运动问题——求出物体运动的加速度——根据具体问题选择用常规分解法还是特殊分解法求解。
(4)类抛体运动
当物体在巨力作用下运动时,若物体的初速度不为零且与外力不在一条直线上,物体所做的运动就是类抛体运动。
在类抛体运动中可采用正交分解法处理问题,基本思路为:
①建立直角坐标系,将外力、初速度沿这两个方向分解。
②求出这两个方向上的加速度、初速度。
③确定这两个方向上的分运动性质,选择合适的方程求解。
功:
1、功的定义:力和作用在力的方向上通过的位移的乘积。是描述力对空间积累效应的物理量,是过程量。
2、功的两个必要因素:作用在物体上的力;物体在力的方向上发生的位移。
3、功的定义式:W=Fscosα,其中F是恒力,s是作用点的位移,α是力与位移间的夹角(功的单位焦耳,简称焦,符号J)。
4、功的计算
①恒力的功可根据W=FScosα进行计算,本公式只适用于恒力做功;
②根据W=P·t,计算一段时间内平均做功;
③利用动能定理计算力的功,特别是变力所做的功;
④根据功是能量转化的量度反过来可求功。
力做功情况的判定方法:
一个力对物体做不做功,是做正功还是做负功,判断的方法是:
(1)看力与位移之间的夹角,或者看力与速度之间的夹角:为锐角时,力对物体做正功;为钝角时,力对物体做负功;为直角时,力对物体不做功。
(2)看物体间是否有能量转化:若有能量转化,则必定有力做功。此方法常用于相连的物体做曲线运动的情况。
变力做功的求法:
公式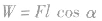 只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
1.用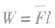 求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用
求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用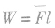 求变力F所做的功。其平均值大小 为
求变力F所做的功。其平均值大小 为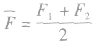 ,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
2.用微元法(或分段法)求变力做功变力做功时,可将整个过程分为几个微小的阶段,使力在每个阶段内不变,求出每个阶段内外力所做的功,然后再求和。当力的大小不变而方向始终与运动方向间的夹角恒定时,变力所做的功形: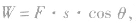 其中s是路程。
其中s是路程。
3.用等效法求变力做功若某一变力做的功等效于某一恒力做的功,则可以应用公式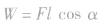 来求。这样,变力做功问题就转化为了恒力做功问题。
来求。这样,变力做功问题就转化为了恒力做功问题。
4.用图像法求变力做功存F—l图像中,图线与两坐标轴所围“面积”的代数和表示F做的功,“面积”有正负,在l轴上方的“面积”为正,在l轴下方的“面积”为负。
5.应用动能定理求变力做功
如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能变化量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
6.利用功能关系求变力做功
在变力做功的过程中,当有重力势能、弹性势能以及其他形式的能量参与转化时,可以考虑用功能关系求解。因为做功的过程就是能量转化的过程,并且转化过程中能量守恒。
7.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是恒定的。若功率P是变化的,则需用 计算,其中当P随时间均匀变化时,
计算,其中当P随时间均匀变化时, 。
。
与“如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的...”考查相似的试题有:
- 在H高处以水平速度V0抛出一物,着地时的速度与水平面夹角为α,以下哪一组V0与H值可使α值最大[ ]A.V0=20m/s,H=30mB.V0=50m/s...
- 长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点正下方处,以一定初速度水平向右抛出,经一定时间绳被拉直...
- 两个相同直角斜面, 已知底边长度是竖直边长度的2倍,如图固定水平面上,小球从左边斜面的顶点以不同的初速度水平向右抛出小球...
- 如图所示,排球网高为H,半场长为L,运动员扣球点高为h,扣球点离网水平距离为s。若运动员扣出的球水平飞出,且落在对方半场...
- (8分)如图所示,在距地面2高空A处以水平初速度v0=投掷飞镖,在与A点水平距离为的水平地面上的B点有一个气球,选择适当时机...
- 某同学在某砖墙前的高处水平抛出一石子,石子在空中运动的部分轨迹照片如图所示。从照片可看出石子恰好垂直打在一倾角为370的...
- 如图所示,足够长的平直轨道MN上有一点C,过MN的竖直平面上有两点A,B,A点在C点的正上方,B点与A点在一条水平线上,不计轨道...
- 如图所示,在倾角为θ的光滑斜面上的A点处,以初速度v1水平抛出一个小物体a,同时小物体b以初速度v2沿斜面下滑,两物体同时到...
- 物体做直线运动的v-t图象如图所示,已知第1s内合外力对物体做的功为W,则从第5s末到第7s末合外力做功为A.–WB.WC.2WD.4W
- 空间某一静电场的电势Φ在x轴上分布如图所示,x轴上两点B、C点电场强度在x方向上的分量分别是EBx、ECx,下列说法中正确的有( ...