本试题 “如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,筒内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半,内壁上有一质量为m的小物块。求...” 主要考查您对圆锥摆
力的分解
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 圆锥摆
- 力的分解
圆锥摆的知识:
圆锥摆模型的结构特点——一根质量和伸长可以不计的线,系一个可以视为质点的摆球,在水平面内做匀速圆周运动,且在摆线沿顶点位置不变的圆锥面上运动。
圆锥摆的特点:
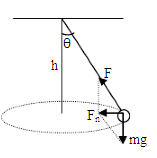
1、圆锥摆模型的受力特点——只受两个力:竖直向下的重力(mg)和沿摆线方向的拉力(F),二力的合力就是摆球做圆周运动的向心力(Fn),如图所示。
2、向心力和向心加速度的计算
设摆球的质量为m,摆长为l,与竖直方向的夹角为θ,摆球的线速度、角速度、周期和频率依次为v、ω、T和f。如图所示,根据不同的条件
向心力可以表示为: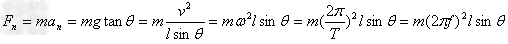 ;
;
向心加速度可表示为: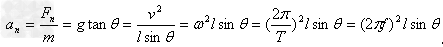 。
。
3、摆线拉力的计算计算
摆线的拉力,有两种基本思路:
①当θ角已知时,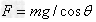 ;
;
②当θ角未知时,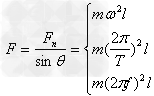 。
。
4、周期T、频率f和角速度ω的计算
根据向心加速度公式,有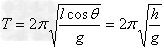 ,
,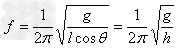 ,
, 。式中
。式中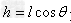 为摆球的轨道平面到悬点的距离,即圆锥摆的高度。由这些公式可知,高度相同的圆锥摆,即等高圆锥摆的T、f和ω相等,与m、l和θ无关。
为摆球的轨道平面到悬点的距离,即圆锥摆的高度。由这些公式可知,高度相同的圆锥摆,即等高圆锥摆的T、f和ω相等,与m、l和θ无关。
5、漏斗摆:物体在光滑的漏斗形容器内壁的某水平面上做匀速圆周运动。漏斗摆的力学特点:物体只受两个力,竖直向下的重力mg,垂直于漏斗壁的弹力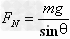 ,两个力的合力水平指向转轴,其向心力
,两个力的合力水平指向转轴,其向心力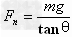 。如图所示。
。如图所示。
①向心加速度的计算 ,θ角一定,故an恒定。
,θ角一定,故an恒定。
②周期T、角速度ω、线速度v的计算(设匀速圆周运动的平面离漏斗尖端距离为h)
由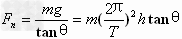 ,得
,得 ;
;
由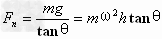 ,得
,得 ;
;
由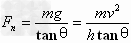 ,得
,得 。
。
可见,h增大,线速度增大,角速度减小,周期增大。
结构特点:
一根质量和伸长可以不计的线,系一个可以视为质点的摆球,在水平面内作匀速圆周运动。
受力特点:
只受两个力:竖直向下的重力 mg 和沿摆线方向的拉力 F 。两个力的合力,就是摆球作圆周运动的向心力 F n
力的合成与分解:
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
分解方法:
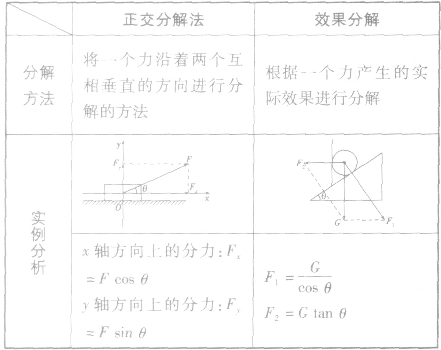
几种按效果分解的实例:


由力的三角形定则求力的最小值:
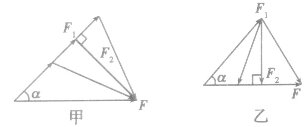
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值 。
。
(2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值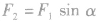 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值 。
。
由圆的切线求力方向的极值:
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足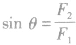 。
。 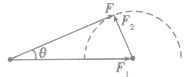
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足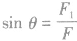 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足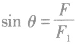 。
。
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
力的分解的几种情况:
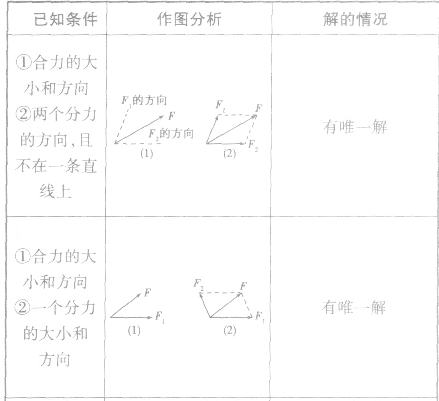
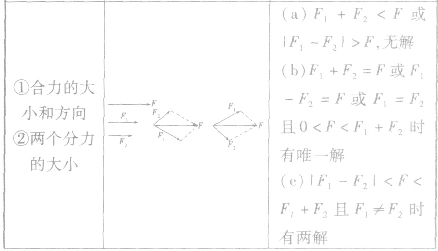
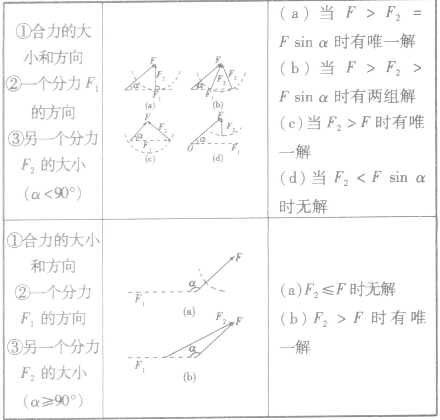
分解方法:

几种按效果分解的实例:


由力的三角形定则求力的最小值:
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值
 。
。 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值
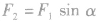 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值
 。
。由圆的切线求力方向的极值:
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足
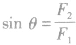 。
。 
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足
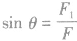 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足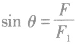 。
。
发现相似题
与“如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,筒内壁...”考查相似的试题有:
- 如图所示的圆锥摆中,摆球在水平面上作匀速圆周运动,关于的受力情况,下列说法中正确的是( )A.摆球受重力、拉力和向心力...
- 如图所示,将一根长为L的不可伸长的轻质绳子分成等长的两段,绳子的一端悬挂于水平天花板上,另一端共同吊起一个重力为G的物...
- 如图所示,挑水时,水桶上绳子分别为a、b、c三种状况,则绳子在______种情况下容易断。
- 如图所示,A、B两物体的质量分别是mA和mB,整个系统处于静止状态,滑轮的质量和一切摩擦不计。如果绳的一端由P点缓慢向左运动...
- 两个共点力,大小都是50N,如果要使这两个力的合力也是50N,则这两个力的夹角应该为:( )A B C D
- 一只船在静水中的速度为4m/s,它要横渡一条40m宽的河,水流速度为3m/s,下列说法正确的是( )A.船过河的位移一定为40mB.船...
- B、C两个小球重量均为G,用细线悬挂在竖直墙上的A、D两点。细线与竖直墙壁之间的夹角分别为30o和60o(见图中标注),两个小球...
- 如图所示, 用绳索将重球挂在墙上,不考虑墙的摩擦。如果把绳的长度增加一些,则球对绳的拉力F1和球对墙的压力F2的变化情况是...
- 两根长度相等的轻绳,下端挂着质量为m的物体,上端分别固定在水平天花板上的MN两点,MN两点间的距离为s,如图所示,已知两绳...
- 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,...