本试题 “将一摆长为2m的单摆放在某一星球表面,测得完成60次全振动所用时间为120s,求:(1)该星球表面的重力加速度;(2)若该星球的半径与地球半径相同,则地球与...” 主要考查您对计算天体质量与密度
单摆的周期
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 计算天体质量与密度
- 单摆的周期
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。以地球的质量的计算为例
①若已知月球绕地球做匀速圆周运动的周期T和半径r,根据: 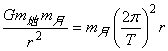 ,得:
,得:![]() ;
;
②若已知月球绕地球做匀速圆周运动的线速度v和半径r,根据: ![]() ,得:
,得:![]() ;
;
③若已知月球绕地球做匀速圆周运动的线速度v和周期T,根据: ![]() 和
和![]() ,得:
,得:![]() ;
;
④若已知地球的半径R和地球表面的重力加速度g,根据: ![]() ,得:
,得:![]() ——此式通常被称为黄金代换式。
——此式通常被称为黄金代换式。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
天体球体积:V=![]() ;天体密度:
;天体密度:![]() (由
(由![]() ,
,![]() ,
,![]() ,r指球体半径,R指轨道半径,当R=r时,
,r指球体半径,R指轨道半径,当R=r时,![]() )。
)。
知识点拨:
科学真是迷人.地球、太阳等天体的质量是多少?天平无法测量.但在我们学习了万有引力定律之后,我们便可以通过它来"称量".求天体质量和密度方法:在地面附近万有引力近似等于物体的重力.由于地球的自转,因而地球表面上的物体随地球自转时需要向心力.所以重力实际上只是万有引力的一个分力,另一个分力就是物体随地球自转时需要的向心力,这个分力与万有引力相比很小忽略不计,可近似认为万有引力等于物体的重力。
1.定义:用一根不可伸长且没有质量的细线悬挂一质点所组成的装置,叫做单摆,它是实际摆的理想化模型
2.模型条件:
(1)摆线的形变量与摆线长度相比小得多,摆线的质量与摆球质量相比小得多,这时可把摆线看成是不可伸长,且没有质量的细线。
(2)摆球的大小与摆线长度相比小得多,这时可把摆球看成是没有大小只有质量的质点。
(3)忽略空气对它的阻力。某一物理量是否可以略去不计,是相对而言的。为了满足上述条件及尽量减小空气阻力对它的影响,我们组成单摆的摆球应选择质量大而体积小的球,摆线应尽量选择细而轻目弹性小的线
3.平衡位置:摆球静止时所处的位置即最低点
4.简谐运动条件:

5.单摆的周期公式:
①在振幅很小的条件下,单摆的振动周期跟振幅无关;
②单摆的振动周期跟摆球的质量无关,只与摆长L和当地的重力加速度g有关;
③摆长L是指悬点到摆球重心间的距离,在某些变形单摆中,摆长L应理解为等效摆长,重力加速度应理解为等效重力加速度(一般情况下,等效重力加速度g'等于摆球静止在平衡位置时摆线的张力与摆球质量的比值)。
单摆问题中的等效处理方法:
单摆的周期公式 是惠更斯从实验中总结出来的。单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力,偏角越大回复力越大,加速度 (
是惠更斯从实验中总结出来的。单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力,偏角越大回复力越大,加速度 ( )越大。由于摆球的轨迹是圆弧,所以除最高点外,摆球的回复力并不等于合外力。在有些振动系统中l不一定是绳长,g也不一定为9.8m/s2,因此出现了等效摆长和等效重力加速度的问题。
)越大。由于摆球的轨迹是圆弧,所以除最高点外,摆球的回复力并不等于合外力。在有些振动系统中l不一定是绳长,g也不一定为9.8m/s2,因此出现了等效摆长和等效重力加速度的问题。
1.等效摆长
摆长是指摆动圆弧的圆心到撰球重心的距离,而不一定为摆绳的长。如图中,摆球可视为质点,各段绳长均为Z,甲、乙摆球做垂直纸面的小角度摆动,丙摆球在纸面内做小角度摆动,O'为垂直纸面的钉子,而且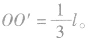

甲:等效摆长
乙:等效摆长
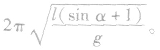
丙:摆绳摆到竖直位置时,圆弧圆心就由O变为O',摆球振动时,半个周期摆长为l,另半个周期摆长为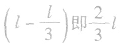 ,则单摆丙的周期为
,则单摆丙的周期为
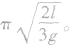
2.等效重力加速度不一定等于9.8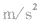
(1)g由单摆所在的空间位置决定。g随所在地球表面的位置和高度的变化而变化,纬度越低,高度越高,g的值就越小,另外,在不同星球上管也不同。
(2)g还由单摆系统的运动状态决定,如单摆处在向上加速的升降机中,设加速度为a,则摆球处于超重状态,沿圆弧的切向分力变大,则重力加速度的等效值 若升降机加速下降,则
若升降机加速下降,则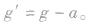 单摆若在沿轨道运行的卫星内,摆球完全失重,回复力为零,等效值
单摆若在沿轨道运行的卫星内,摆球完全失重,回复力为零,等效值 ,摆球不摆动,周期无穷大。
,摆球不摆动,周期无穷大。
(3)一般情况下,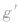 值等于摆球相对于加速系统静止在平衡位置时(平衡位置是指回复力为零的位置,而不是合力为零的位置,也可以说成是让摆球不摆时的位置)重力加速度的等效值,等于摆绳所受的张力与摆球质量的比值即
值等于摆球相对于加速系统静止在平衡位置时(平衡位置是指回复力为零的位置,而不是合力为零的位置,也可以说成是让摆球不摆时的位置)重力加速度的等效值,等于摆绳所受的张力与摆球质量的比值即
但需注意如果在不引起回复力变化的情况,上述方法并不适用,如摆球带电,再在悬点处固定一带电小球,两球之间的静电力不引起回复力的变化,单摆振动周期并不变。
与“将一摆长为2m的单摆放在某一星球表面,测得完成60次全振动所...”考查相似的试题有:
- 2007年10月24日,我国“嫦娥一号”探月卫星成功发射。“嫦娥一号”卫星开始绕地球做椭圆轨道运动,经过变轨、制动后,成为一颗绕...
- 已知万有引力恒量G,则还需知道下面哪一选项的数据,就可以计算地球的质量[ ]A.已知地球绕太阳运行的周期及地球中心到太阳中...
- 在某星球表面以初速度v0竖直上抛一个物体,若忽略其它力的影响,设物体只受该星球引力作用,该物体上升的最大高度为h,已知该...
- 摆长为L的单摆做简谐振动,若从某时刻开始计时,取作t=0,当振动至时,摆球具有负向最大速度,则单摆的振动图象是图中的[ ]A...
- (1)甲同学想在家里做用单摆测定重力加速度的实验,但没有合适的摆球,他找到了一块大小为3cm左右,外形不规则的大理石块代...
- 对单摆的振动,以下说法中正确的是 ( )A.单摆摆动时,摆球受到的向心力大小处处相等B.摆球经过平衡位置时所受合外力为零C...
- 图11-4-5中两单摆摆长相同,平衡时两摆球刚好接触,现将摆球A在两摆球所在平面内向左拉开一小角度后释放,碰撞后,两摆球分开...
- 如图所示为一单摆及其振动图象,由图回答:单摆的振动频率为______Hz,;一周期内位移最大的时刻为______和______.若摆球从E...
- (选修3-4选做题)关于振动和波动,下列说法正确的是[ ]A.单摆做简谐运动的周期与摆球的质量有关B.部队过桥不能齐步走而要...
- 关于单摆的摆球运动时所受的力和能量转化,下列说法中正确的是( )A.摆球从A运动到B的过程中,重力做的功等于动能的增量B....