以下装置中，利用杠杆平衡原理的装置是（） A．斜面 B．液压机 C．天平 D．连通器,初中,物理试题,帕斯卡原理及其应用考点,连通器原理及应用考点,杠杆的动态平衡分析考点,好技网

单选题
以下装置中，利用杠杆平衡原理的装置是（）

A．斜面 B．液压机 C．天平 D．连通器

本题信息：物理单选题难度一般来源:未知
本题答案
查看答案

本试题 “以下装置中，利用杠杆平衡原理的装置是（） A．斜面 B．液压机 C．天平 D．连通器” 主要考查您对
帕斯卡原理及其应用

连通器原理及应用

杠杆的动态平衡分析
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

帕斯卡原理及其应用
连通器原理及应用
杠杆的动态平衡分析

帕斯卡原理:
加在密闭液体上的压强，能够大小不变地被液体向各个方向传递，这个规律被称为帕斯卡原理。帕斯卡原理揭示了液体压强的传递规律，是许多液压系统和液压机工作的基础。如用于维修汽车的液压千斤顶 (如图)，汽车的液压刹车系统，铲车等部用了液压技术。

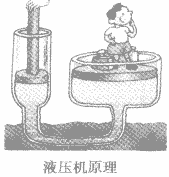
液压机的工作原理如图所示，两个活塞，与同一容器的液体相接触。施加于小活塞的压强被液体传递给大活塞，大活塞便可以产生一个与其表面面积成正比的力。

帕斯卡:
     帕斯卡发现了液体传递压强的基本规律，这就是著名的帕斯卡定律．所有的液压机械都是根据帕斯卡定律设计的，所以帕斯卡被称为“液压机之父”．

     通过观察，帕斯卡设计了“帕斯卡球”实验，帕斯卡球是一个壁上有许多小孔的空心球，球上连接一个圆筒，筒里有可以移动的活塞．把水灌进球和筒里，向里压活塞，水便从各个小孔里喷射出来了，成了一支“多孔水枪” 帕斯卡球的实验证明，液体能够把它所受到的压强向各个方向．通过观察发现每个孔喷出去水的距离差不多，这说明，每个孔所受到的压强都相同。
     在初中阶段，液体压强原理可表述为：“液体内部向各个方向都有压强，压强随液体深度的增加而增大，同种液体在同一深度的各处，各个方向的压强大小相等；不同的液体，在同一深度产生的压强大小与液体的密度有关，密度越大，液体的压强越大。”

     特点：加在封闭液体上的压强能够大小不变地被液体向各个方向传递。同种液体在同一深度液体向各个方向的压强都相等。

裂桶实验：
     帕斯卡在1648年表演了用一个著名的实验：他用一个密闭的装满水的桶，在桶盖上插入一根细长的管子，从楼房的阳台上向细管子里灌水。结果只到了几杯水，桶就裂了，桶里的水就从裂缝中流了出来。原来由于细管子的容积较小，几杯水灌进去，其深度h很大。一个容器里的液体，对容器底部(或侧壁)产生的压力远大于液体自身所受的重力。

定义：
上端开口，下端连通的容器叫连通器，如图所示。

特点：
连通器里的同种液体不流动时，各容器中的液面总保持相平。

应用：
乳牛自动喂水器、茶壶、锅炉水位计、船闸等。如图所示。

说明：
(1)连通器的特点既可以通过实验归纳得出，也可以通过理论推导得出。
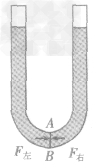
(2)理论推导的过程(建立模型法)：如图，液体不流动一液片处于平衡状态一液片两侧受到的压力相等(F左=F右)→液片两侧受到的压强相等(p左=P右)→两管液面高度相等(h左=h右)→两管液面相平。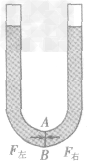

(3)连通器特点应用：连通器的特点是只有容器内装有同一种液体时各个容器中的液面才是相平的。如果容器倾斜，则各容器中的液体即开始流动，由液柱高的一端向液柱低的一端流动，直到各容器中的液面相平时，才停止流动。

压强计：
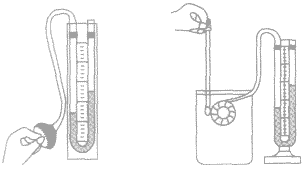
压强计是测量液体内部压强的仪器(如图所示)，它由探头，U形管，软管组成，当探头的薄膜(橡皮模) 受压强的作用时，U形管左右两侧液面就会产生高度差，液面高度差越大，薄膜(橡皮模)受到的压强越大。

船闸:
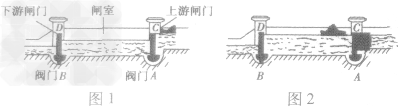
船闸是利用连通器原理T作的。通过闸门和阀门的打开、关闭，调节船闸内的水位分别与上、下游水位相平，使船经过船闸从上游驶往下游或从下游驶往上游。当上游闸门打开时，闸室与上游河流构成连通器；当下游闸门打开时，闸室与下游河流构成连通器，这样使落差较大的河面上能让船只正常安全地行驶。下面描述的是一艘轮船由上游通过船闸驶往下游的情况。
(1)如图l船在上游(打开上游阀门A，闸室和上游水道构成了一个连通器)。
(2)如图2船进入闸室中(闸室水面上升到和上游水面相平后，打开上游闸门，船驶入闸室)。
(3)如图3船准备出闸室(打开下游阀门B，闸室和下游水道构成了一个连通器)。

杠杆的平衡状态：
杠杆静止不动或匀速转动都叫做杠杆平衡，注意我们在实验室所做的杠杆平衡条件的实验，是在杠杆水平位置平衡进行的，但在实际生产和生活中，这样的平衡是不多的，在许多情况下，杠杆是倾斜静止的，这是因为杠杆受到平衡力作用。所以说杠杆不论处于怎样的静止，都可以理解成处于平衡状态。

杠杆动态平衡问题：
杠杆动态平衡的几种类型杠杆动态平衡是指构成杠杆的某些要素发生变化,而杠杆仍处于静止状态或匀速转动状态，
分析杠杆的动态平衡时，一般是动中取静，根据杠杆平衡条件，分析比较，得出结论。下面就杠杆动态平衡问题归类分析。

一、阻力一定，判断动力的变化情况
1、l₁不变，l₂变化
例1、如图1所示，轻质杠杆可绕O转动，在A点始终受一垂直作用于杠杆的力，在从A转动A/位置时，力F将（）
A、变大
B、变小
C、先变大，后变小
D、先变小，后变大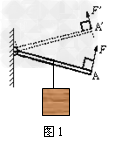

分析：当杠杆在水平面以下上升到水平面上时，l₁不变，l₂增大，由，F增大，当杠杆从水平面继续上升过程中，l₂减小，所以F减小。
2、l₂不变，l₁变化
例2、如图2所示，轻质杠杆OA的B点挂着一个重物，A端用细绳吊在圆环M下，此时OA恰成水平且A点与圆弧形架PQ的圆心重合，那么当环M从P点逐渐滑至Q点的过程中，绳对A端的拉力大小将（）
A、保持不变
B、逐渐增大
C、逐渐减小
D、由大变小再变大

分析：当M点从P点滑至Q点的过程中，我们分两个过程分析，
一是从P点滑至竖直位置，动力臂l₁逐渐增大（同学们不妨作出这两点的动力臂），由知F逐渐变小；
二是从竖直位置到Q点，动力臂逐渐减小，所以又逐渐增大。故选D。

3、l₁与l₂同时变化，但比值不变
例3、用图3所示的杠杆提升重物，设作用在A端的力F始终竖直向下，在将重物慢慢提升到一定高度的过程中，F的大小将（）
A、保持不变
B、逐渐变小
C、逐渐变大
D、先变大，后变小

分析：：F始终竖直向下，与阻力作用线平行，分别作出F与G的力臂l₁和l₂，构建两个相似三角形（同学们不妨在图中作出），可以看出，
为定值，由杠杆平衡条件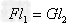，，得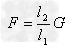，所以，F大小不变。

4、l₁与l₂同时变化
例4、如图4所示，一个直杠杆可绕轴O转动，在直杆的中点挂一重物，在杆的另一端施加一个方向始终保持水平的力F，将直杆从竖直位置慢慢抬起到水平位置过程中，力F大小的变化情况是（）
A、一直增大
B、一直减小
C、先增大后减小
D、先减小后增大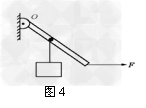

分析：将直杆从竖直位置慢慢抬起到水平位置过程中，l₁变小，l₂变大，由知，F一直在增大。
二、动力与阻力不变，动力臂与阻力臂变化
例5、如图5所示，用一细线悬挂一根粗细均匀的轻质细麦桔杆，使其静止在水平方向上， O为麦桔杆的中点．这时有两只蚂蚁同时从O点分别向着麦桔杆的两端匀速爬行，在蚂蚁爬行的过程中麦桔杆在水平方向始终保持乎衡，则（）
A、两蚂蚁的质量一定相等
B、两蚂蚁的爬行速度大小一定相等
C、两蚂蚁的质量与爬行速度大小的乘积一定相等
D、两蚂蚁对麦桔杆的压力一定相等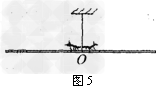

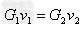分析：蚂蚁爬行的过程中麦桔杆始终保持乎衡，有，即，所以。故选C。

三、动力臂与阻力臂不变，动力与阻力改变
例6、如图6所示的轻质杠杆，AO小于BO．在A、B两端悬挂重物（同种物质）G₁和G₂后杠杆平衡．若将G₁和G₂同时浸没到水中则（）
A、杠杆仍保持平衡
B、杠杆的A端向下倾斜
C、杠杆的B端向下倾斜
D、无法判断

分析：在空气中，杠杆平衡，故有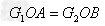；G₁和G₂同时浸没到水中，有，说明杠杆仍然平衡。故选A。

杠杆的转动：
判断杠杆平衡的依据是：“动力×动力臂”是否等于“阻力×阻力臂”。若二者相等，杠杆平衡；若二者不相等，则杠杆不平衡，且杠杆会向“乘积”大的一方倾斜。
例如图所示，杠杆在水平位置处于平衡状态，杠杆上每格均匀等距，每个钩码都相同。下列四项操作中，会使杠杆左端下倾的是( )

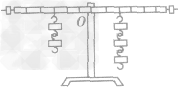
①在杠杆的两侧同时各减掉一个钩码；②在杠杆的两侧钩码下同时各加挂一个相同的钩码；④将杠杆两侧的钩码同时各向外移动一个小格；④将杠杆两侧的钩码同时各向内移动一个小格。
A．①③B．②④C．②③D．①④

解析根据杠杆的平衡条件，当左边力与力臂的乘积等于右边力与力臂的乘积时，杠杆平衡。哪一边乘积大，哪一边下降，可对本题四种情况逐一分析，最后作出判断。

答案B

发现相似题

与“以下装置中，利用杠杆平衡原理的装置是（） A．斜面 B．液压...”考查相似的试题有：