本试题 “如图一,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE...” 主要考查您对全等三角形的性质
正方形,正方形的性质,正方形的判定
垂直平分线的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 全等三角形的性质
- 正方形,正方形的性质,正方形的判定
- 垂直平分线的性质
两个全等的三角形,而该两个三角形的三条边及三个角都对应地相等。全等三角形是几何中全等的一种。根据全等转换,两个全等三角形可以是平移、旋转、轴对称,或重叠等。当两个三角形的对应边及角都完全相对时,该两个三角形就是全等三角形。正常来说,验证两个全等三角形时都以三个相等部分来验证,最后便能得出结果。
全等三角形的对应边相等,对应角相等。
①全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
②全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
③有公共边的,公共边一定是对应边;
④有公共角的,角一定是对应角;
⑤有对顶角的,对顶角一定是对应角。
全等三角形的性质:
1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
8.全等三角形的对应角的三角函数值相等。
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
特殊的长方形。
四条边都相等且四个角都是直角的四边形叫做正方形。
有一组邻边相等的矩形是正方形。
有一个角为直角的菱形是正方形。
对角线平分且相等,并且对角线互相垂直的四边形为正方形。
对角线相等的菱形是正方形。
正方形的性质:
1、边:两组对边分别平行;四条边都相等;相邻边互相垂直
2、内角:四个角都是90°;
3、对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;
4、对称性:既是中心对称图形,又是轴对称图形(有四条对称轴);
5、正方形具有平行四边形、菱形、矩形的一切性质;
6、特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;
正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
7、在正方形里面画一个最大的圆,该圆的面积约是正方形面积的78.5%;
正方形外接圆面积大约是正方形面积的157%。
8、正方形是特殊的长方形。
正方形的判定:
判定一个四边形为正方形的一般顺序如下:先证明它是平行四边形,再证明它是菱形(或矩形),最后证明它是矩形(或菱形)。
1:对角线相等的菱形是正方形。
2:有一个角为直角的菱形是正方形。
3:对角线互相垂直的矩形是正方形。
4:一组邻边相等的矩形是正方形。
5:一组邻边相等且有一个角是直角的平行四边形是正方形。
6:对角线互相垂直且相等的平行四边形是正方形。
7:对角线相等且互相垂直平分的四边形是正方形。
8:一组邻边相等,有三个角是直角的四边形是正方形。
9:既是菱形又是矩形的四边形是正方形。
有关计算公式:
若S为正方形的面积,C为正方形的周长,a为正方形的边长,则
正方形面积计算公式:S =a×a(即a的2次方或a的平方),或S=对角线×对角线÷2;
正方形周长计算公式: C=4a 。
S正方形= 。(正方形边长为a,对角线长为b)
。(正方形边长为a,对角线长为b)
垂直于一条线段并且平分这条线段的直线,叫做这条线段的垂直平分线(中垂线)。
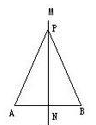
如图:直线MN即为线段AB的垂直平分线。
垂直平分线的性质:
1.垂直平分线垂直且平分其所在线段。
2.垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
3.如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。
4.三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相 等。
(此时以外心为圆心,外心到顶点的长度为半径,所作的圆为此三角形的外接圆。)
判定:
①利用定义;
②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(即线段垂直平分线可以看成到线段两端点距离相等的点的集合)
尺规作法:(用圆规作图)
1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。
2、分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线。得到两个交点(两交点交与线段的异侧)。
3、连接这两个交点。
原理:等腰三角形的高垂直平分底边。
与“如图一,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D...”考查相似的试题有:
- 如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD,过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF。(1)求EG的...
- 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等。一条直线l与方形环的边线有...
- 如图,已知四边形ABCD是菱形,点E,F分别是边CD,AD的中点。求证:AE=CF。
- 一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ACB的斜边AB的中点处,设AC=BC=a.(1)如...
- 已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长。
- 已知:如图,O为□ABCD的对角线AC的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.(1)图中共有...
- 如图,△ABC≌△AEF,∠EAC=30°,求∠BAF的度数。
- 如图,在正方形ABCD中,点E、F分别是边AB、AD的中点,DE与CF相交于G,DE、CB的延长线相交于点H,点M是CG的中点.求证:(1)B...
- 如图有一直角∠A。(1)用尺规作图作出∠A的角平分线,并在该角平分线上取一点C。(保留作图痕迹,不写作法,不证明。)(2)用...
- 到△ABC三个顶点距离相等的点是△ABC的( ) A.三条角平分线的交点 B.三条中线的交点 C.三条高的交点 D.三条垂直平分线的交点