本试题 “如图,△ABC在8×8的方格中位置如图所示,A(1,4), B(-2,2),(1)请你在方格中建立直角坐标系,并写出C点的坐标;(2)把△ABC向下平移1个单位后,再向右...” 主要考查您对三角形的周长和面积
用坐标表示位置
平移
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角形的周长和面积
- 用坐标表示位置
- 平移
三角形的概念:
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。
三角形的分类:
(1)三角形按边的关系分类如下:
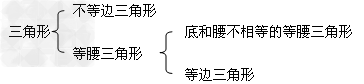 ;
;
(2)三角形按角的关系分类如下:

把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。
三角形的分类:
(1)三角形按边的关系分类如下:
 ;
;(2)三角形按角的关系分类如下:

把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
点的坐标的概念:
点的坐标用(a,b)表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当a≠b时,(a,b)和(b,a)是两个不同点的坐标。
各象限内点的坐标的特征 :
点P(x,y)在第一象限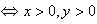 ;点P(x,y)在第二象限
;点P(x,y)在第二象限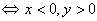
点P(x,y)在第三象限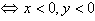 ;点P(x,y)在第四象限
;点P(x,y)在第四象限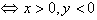
坐标轴上的点的特征:
点P(x,y)在x轴上 y=0,x为任意实数
y=0,x为任意实数
点P(x,y)在y轴上 x=0,y为任意实数
x=0,y为任意实数
点P(x,y)既在x轴上,又在y轴上 x,y同时为零,即点P坐标为(0,0)。
x,y同时为零,即点P坐标为(0,0)。
点P(x,y)到坐标轴及原点的距离:
(1)点P(x,y)到x轴的距离等于|y|;
(2)点P(x,y)到y轴的距离等于|x|;
(3)点P(x,y)到原点的距离等于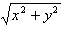 。
。
坐标表示位置步骤:
利用平面直角坐标系绘制区域内一些地点分布情况的平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确定X轴、y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
点的坐标用(a,b)表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当a≠b时,(a,b)和(b,a)是两个不同点的坐标。
各象限内点的坐标的特征 :
点P(x,y)在第一象限
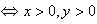 ;点P(x,y)在第二象限
;点P(x,y)在第二象限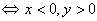
点P(x,y)在第三象限
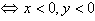 ;点P(x,y)在第四象限
;点P(x,y)在第四象限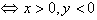
坐标轴上的点的特征:
点P(x,y)在x轴上
 y=0,x为任意实数
y=0,x为任意实数 点P(x,y)在y轴上
 x=0,y为任意实数
x=0,y为任意实数 点P(x,y)既在x轴上,又在y轴上
 x,y同时为零,即点P坐标为(0,0)。
x,y同时为零,即点P坐标为(0,0)。 点P(x,y)到坐标轴及原点的距离:
(1)点P(x,y)到x轴的距离等于|y|;
(2)点P(x,y)到y轴的距离等于|x|;
(3)点P(x,y)到原点的距离等于
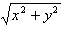 。
。 坐标表示位置步骤:
利用平面直角坐标系绘制区域内一些地点分布情况的平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确定X轴、y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
定义:
将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移是图形变换的一种基本形式。平移不改变图形的形状和大小,平移可以不是水平的。
平移作图的步骤:
(1)找出能表示图形的关键点;
(2)确定平移的方向和距离;
(3)按平移的方向和距离确定关键点平移后的对应点;
(4)按原图的顺序,连结各对应点。
将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移是图形变换的一种基本形式。平移不改变图形的形状和大小,平移可以不是水平的。
平移基本性质:
经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;
平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
(1)图形平移前后的形状和大小没有变化,只是位置发生变化;
(2)图形平移后,对应点连成的线段平行(或在同一直线上)且相等
(3)多次连续平移相当于一次平移。
(4)偶数次对称后的图形等于平移后的图形。
(5)平移是由方向和距离决定的。
这种将图形上的所有点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移
平移的条件:确定一个平移运动的条件是平移的方向和距离。
平移的三个要点
1 原来的图形的形状和大小和平移后的图形是全等的。
2 平移的方向。(东南西北,上下左右,东偏南n度,东偏北n度,西偏南n度,西偏北n度)
3 平移的距离。(长度,如7厘米,8毫米等)
平移作用:
1.通过简单的平移可以构造精美的图形。也就是花边,通常用于装饰,过程就是复制-平移-粘贴。
2.平移长于平行线有关,平移可以将一个角,一条线段,一个图形平移到另一个位置,是分散的条件集中到一个图形上,使问题得到解决。
平移作图的步骤:
(1)找出能表示图形的关键点;
(2)确定平移的方向和距离;
(3)按平移的方向和距离确定关键点平移后的对应点;
(4)按原图的顺序,连结各对应点。
发现相似题
与“如图,△ABC在8×8的方格中位置如图所示,A(1,4), B(-2,2...”考查相似的试题有:
- 在点(0,0),(1,0),(0,2),(1,2),(-1,2)(-2,3)中,不属于任何象限的点有( )A.2个B.3个C.4个D.5个
- 若点与点关于x轴对称,则的值分别是( )A.B.C.D.
- 如果用(7,1)表示七年级一班,那么八年级四班可表示成______.
- 若小明所在的位置表示为(8,3),小东所在的位置是(2,11),则小明与小东之间相距______.
- 这是一个动物园游览示意图,试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置,(画出图形,并写出各景点的坐标)。
- 如图,将矩形纸片ABCD沿AE向上折叠,使点B落在DC边上的F处,若∠AFD的周长为9,△ECF的周长为3,则矩形ABCD周长为 。
- △ABC在网格中如图所示,请根据下列提示作图并填空.(1)向上平移2个单位长度,再向右移3个单位长度得到△A′B′C′,作出△A′B′C′...
- 下列图案中是轴对称图形的共有:( )A.1个B.2个C.3个D.4个
- 下列图形中,不是轴对称图形的是( )
- 下图所示的四个汽车标志图案中,不能用平移或旋转变换来分析其形成过程的图案是( )A.B.C.D.