本试题 “盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球。规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分。现从盒内任取3个球,(1...” 主要考查您对概率的基本性质(互斥事件、对立事件)
古典概型的定义及计算
离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 概率的基本性质(互斥事件、对立事件)
- 古典概型的定义及计算
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
互斥事件:
事件A和事件B不可能同时发生,这种不可能同时发生的两个事件叫做互斥事件。
如果A1,A2,…,An中任何两个都不可能同时发生,那么就说事件A1,A2,…An彼此互斥。
对立事件:
两个事件中必有一个发生的互斥事件叫做对立事件,事件A的对立事件记做 。
。
注:两个对立事件必是互斥事件,但两个互斥事件不一定是对立事件。
事件A+B的意义及其计算公式:
(1)事件A+B:如果事件A,B中有一个发生发生。
(2)如果事件A,B互斥时,P(A+B)=P(A)+P(B),如果事件A1,A2,…An彼此互斥时,那么P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)。
(3)对立事件:P(A+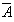 )=P(A)+P(
)=P(A)+P( )=1。
)=1。
概率的几个基本性质:
(1)概率的取值范围:[0,1].
(2)必然事件的概率为1.
(3)不可能事件的概率为0.
(4)互斥事件的概率的加法公式:
如果事件A,B互斥时,P(A+B)=P(A)+P(B),如果事件A1,A2,…An彼此互斥时,那么P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)。
如果事件A,B对立事件,则P(A+B)=P(A)+P(B)=1。
互斥事件与对立事件的区别和联系:
互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生外,还要求二者之一必须有一个发生。因此,对立事件是互斥事件的特殊情况,而互斥事件未必是对立事件,即“互斥”是“对立”的必要但不充分条件,而“对立”则是“互斥”的充分但不必要条件。
基本事件的定义:
一次试验连同其中可能出现的每一个结果称为一个基本事件。
等可能基本事件:
若在一次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件。
古典概型:
如果一个随机试验满足:(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件的发生都是等可能的;
那么,我们称这个随机试验的概率模型为古典概型.
古典概型的概率:
如果一次试验的等可能事件有n个,那么,每个等可能基本事件发生的概率都是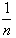 ;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为
;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为 。
。
古典概型解题步骤:
(1)阅读题目,搜集信息;
(2)判断是否是等可能事件,并用字母表示事件;
(3)求出基本事件总数n和事件A所包含的结果数m;
(4)用公式 求出概率并下结论。
求出概率并下结论。
求古典概型的概率的关键:
求古典概型的概率的关键是如何确定基本事件总数及事件A包含的基本事件的个数。
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称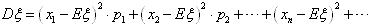 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,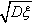 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)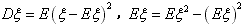 ;
;
(2)若η=aξ+b,则 ;
;
(3)若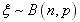 ,则
,则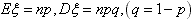 ;
;
(4)若ξ服从几何分布,则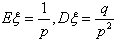 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式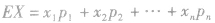 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色...”考查相似的试题有:
- 做一个物理试验,甲、乙两人一次试验成功的概率分别为0.6、0.8,且每次试验成功与否相互之间没有影响,求:(I)甲做试验三次...
- 从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是[ ]A.B.C.D.
- 现在某类病毒记作XmYn,其中正整数m,n(m≤7,n≤9)可以任意选取,则m,n都取到奇数的概率为______.
- 设X是一个离散型随机变量,其分布列为: 则q等于( ) A.1 B.1±C.1-D.1+
- 袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球,ξ表示所取球的标号。(1...
- 抛掷两个骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是( )。
- 某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.(1)设所选3人中女生人数为ξ,求ξ的分布列及数...
- 一个袋中装有10个红球,20个白球,这些球除颜色外完全相同,一次从中摸出5个球,随机变量表示取到的红球数,服从超几何分布,...
- 从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.(1)若抽取后又放回,抽3次,分别求恰2次...
- 2011年3月20日,第19个世界水日,主题是:“城市水资源管理”;2011年“六·五”世界环境日中国主题:“共建生态文明,共享绿色未来...