本试题 “某粮仓是如图所示的多面体,多面体的棱称为粮仓的“梁”.现测得底面ABCD是矩形,AB=16米,AD=4米,腰梁AE、BF、CF、DE分别与相交的底梁所成角均为60°.(1)请...” 主要考查您对柱体、椎体、台体的表面积与体积
异面直线所成的角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 柱体、椎体、台体的表面积与体积
- 异面直线所成的角
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
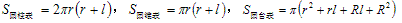
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,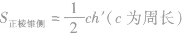 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,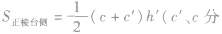  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
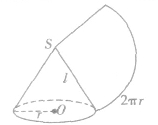 |
圆锥的侧面展开图是扇形: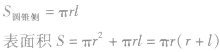 |
 |
| 圆台 |
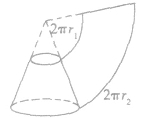 |
圆台的侧面展开图是扇环: |
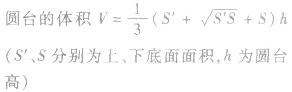 |
| 球 |
 |
 |
 |
异面直线所成角的定义:
直线a、b是异面直线,经过空间任意一点O,分别引直线a′∥a,b′∥b,则把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角,如下图。
两条异面直线所成角的范围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
在异面直线所成角定义中,空间一点O是任取的,而和点O的位置无关。 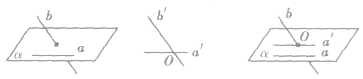
求异面直线所成角的步骤:
A、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选在特殊的位置上。
B、证明作出的角即为所求角;
C、利用三角形来求角。
特别提醒:
(1)两异面直线所成的角与点O(两直线平移后的交点)的选取无关.
(2)两异面直线所成角θ的取值范围是00<θ≤900.
(3)判定空间两条直线是异面直线的方法①判定定理:平面外一点A与平面内一点B的连线和平面内不过点B的直线是异面直线;②反证法:证明两直线共面不可能.
线线角的求法:
(1)定义法:用“平移转化”,使之成为两相交直线所成的角,当异面直线垂直时,应用线面垂直定义或三垂线定理及逆定理判定所成的角为900.
(2)向量法:设两条直线所成的角为θ(锐角),直线l1和l2的方向向量分别为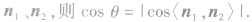
发现相似题
与“某粮仓是如图所示的多面体,多面体的棱称为粮仓的“梁”.现测...”考查相似的试题有:
- 某空间几何体的三视图如下,则它的表面积( )。
- 用一张长12cm,宽8cm的矩形围成圆柱形的侧面,求这个圆柱的体积是( ).
- 正四棱锥的底面边长为2,它的侧棱与底面所成角为60°,则正四棱锥的体积为______.
- 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,,点F是PB的中点,点E在边BC上移动.(1)若,求证:;(2)若二面角的大小为,则CE为...
- 己知某几何体的三视图如图所示,则其体积为[ ]A.4B.8C.D.
- 已知某几何体的三视图如图所示,则它的体积为( )。
- 已知P为△ABC所在平面外的一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点(1)求EF与PC所成的角;(2)求线段EF的长.
- 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的大小是( )(结果用反三角函数值表示)。
- 如图,已知正方体ABCD-A′B′C′D′。(1)哪些棱所在直线与直线BA′是异面直线?(2)直线BA′和CC′的夹角是多少?(3)哪些棱所在...
- 右图的正方体中,M、N是棱BC、CD的中点,则异面直线与MN所成的角为A.30o B. 45o C. 60o D.90o