本试题 “一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:买饭时间(分)12345频率0.10.40.30.10.1从...” 主要考查您对离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 离散型随机变量的期望与方差
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称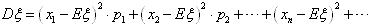 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,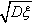 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)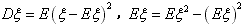 ;
;
(2)若η=aξ+b,则 ;
;
(3)若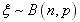 ,则
,则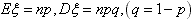 ;
;
(4)若ξ服从几何分布,则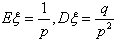 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式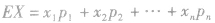 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且...”考查相似的试题有:
- 五名奥运志愿者被随机地分到四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量为这五名志愿者中参加岗位服务的人数...
- 篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球2次(每次罚球结果互不影响...
- 某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有10张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海...
- 设一次随机试验的结果只有A和,且P(A)=m,设随机变量x=则x的方差D(x)是:( )A.4m(1-m) B.2m(1-m) C.m(m-1) D.m(1-m)
- 在10件产品中有2件次品,任意抽取3件,则抽到次品个数的数学期望的值是______.
- 随机变量的概率分布为右表所示,则的值为 。
- (本小题满分12分)根据公安部最新修订的《机动车驾驶证申领和使用规定》:每位驾驶证申领者必须通过《科目一》(理论科目)...
- 箱子里共有10个小球,每个小球被抽取的机会相同,这10个小球中,标记号码为“1”的小球有1个,标记号码为“2”的小球有2个,标记...
- 从分别标有数字1,2,3,…9的9张卡片中任取2张,则两张卡片上数字之和为偶数的概率是______________。
- 小王有一天收到6位好友分别发来的1,2,2,3,3,4条短信,当天他从这6位好友中任取3位的短信阅读,并且只阅读已选取的好友的...