本试题 “(本小题满分12分)两个代表队进行乒乓球对抗赛,每队三名队员,队队员是,队队员是,按以往多次比赛的统计,对阵队员之间的胜负概率如下:对阵队员队队员胜...” 主要考查您对离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 离散型随机变量的期望与方差
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称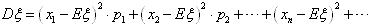 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,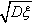 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)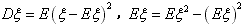 ;
;
(2)若η=aξ+b,则 ;
;
(3)若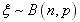 ,则
,则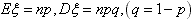 ;
;
(4)若ξ服从几何分布,则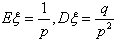 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式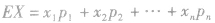 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“(本小题满分12分)两个代表队进行乒乓球对抗赛,每队三名队...”考查相似的试题有:
- 随机的抛掷一枚骰子,所得骰子的点数ξ的数学期望为 .
- (1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,...
- 某市出租车的起步价为6元,行驶路程不超过3km时,租车费为6元,若行驶路程超过3km,则按每超出1km(不足1km也按1km计程)收费...
- 一个口袋中装有标号为1,2,3的6个小球,其中标号1的小球有1个,标号2的小球有2个,标号3的小球有3个,现在口袋中随机摸出2个...
- 为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间...
- 一个袋中有大小、质地相同的标号为的三个小球.某人做如下游戏:每次从袋中摸一个小球,记下标号然后放回,共摸球次.若拿出球...
- 根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3。设各车主购买保险相互独立...
- 为了响应学校“学科文化节”活动,数学组举办了一场数学知识比赛,共分为甲、乙两组.其中甲组得满分的有1个女生和3个男生,乙...
- 一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a、b、c∈(0,1)),已知他投篮一次得分的数学期...
- 已知随机变量ξ+η=8,若ξ~B(10,0.6),则Eη,Dη分别是( ) A.6和2.4 B.2和2.4 C.2和5.6 D.6和5.6