本试题 “已知,, 且(1) 求函数的解析式;(2) 当时,的最小值是-4 , 求此时函数的最大值, 并求出相应的的值.” 主要考查您对向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的含义及几何意义
两个向量的夹角的定义:
对于非零向量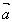 ,
,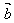 ,作
,作 称为向量
称为向量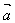 ,
,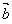 的夹角,当
的夹角,当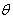 =0时,
=0时,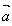 ,
,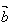 同向,当
同向,当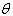 =π时,
=π时,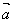 ,
,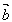 反向,
反向,
当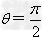 时,
时,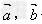 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积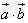 等于
等于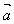 的模
的模 与
与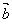 在
在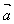 上的投影
上的投影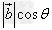 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“已知,, 且(1) 求函数的解析式;(2) 当时,的最小值是-4 , 求...”考查相似的试题有:
- 已知向量,,若与共线,则 ( )A.B.C.D.
- 已知(1,2),,且,则在方向上的投影是( )A.B.C.D.
- 设a,b是非零向量,若函数f(x)=(x a+b)·(a-x b)的图象是一条直线,则必有( )A.a⊥bB.a∥bC.|a|=|b|D.|a|≠|b|
- 已知a=3i+2j-k,b=i-j+2k,其中i、j、k为两两垂直的单位向量则5a与3b的数量积等于______.
- 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN相交于点P,求AP∶PM的值.
- 不共线的两个向量,且与垂直,垂直,与的夹角的余弦值为( )A.B.C.D.
- 已知向量a、b的夹角为120°,且|a|=|b|=4,那么b·(2a+b)的值为( )A.48B.32C.1D.0
- 已知平面向量的夹角为60°,,,则
- 若,,,,则△的面积是 ( )A.1B.2C.D.
- 正的边长为1,设,,,则( ) A.B.C.D.