本试题 “在下列说法中:(1)无限小数都是无理数;(2)如果将一个直角三角形的三边都扩大相同的倍数,所得的三角形仍然是直角三角形;(3)成中心对称的两个图形,对...” 主要考查您对无理数的定义
矩形,矩形的性质,矩形的判定
正方形,正方形的性质,正方形的判定
中心对称
相似图形
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 无理数的定义
- 矩形,矩形的性质,矩形的判定
- 正方形,正方形的性质,正方形的判定
- 中心对称
- 相似图形
即非有理数之实数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。 常见的无理数有大部分的平方根、π和e(其中后两者同时为超越数)等。
无理数是无限不循环小数。如圆周率π、
 等。
等。无理数性质:
无限不循环的小数就是无理数 。换句话说,就是不可以化为整数或者整数比的数
性质1 无理数加(减)无理数既可以是无理数又可以是有理数
性质2 无理数乘(除)无理数既可以是无理数又可以是有理数
性质3 无理数加(减)有理数一定是无理数
性质4 无理数乘(除)一个非0有理数一定是无理数
无理数与有理数的区别:
1、把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,
比如:4=4.0,
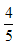 =0.8,
=0.8,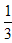 =0.33333……
=0.33333……而无理数只能写成无限不循环小数,
比如:
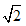 =1.414213562…………
=1.414213562…………根据这一点,人们把无理数定义为无限不循环小数;
2、所有的有理数都可以写成两个整数之比,而无理数不能。根据这一点,有人建议给无理数摘掉,把有理数改叫为“比数”,把无理数改叫为“非比数”。
无理数的识别:
判断一个数是不是无理数,关键就看它能不能写出无限不循环小数,而把无理数写成无限不循环小数,不但麻烦,而且还是我们利用现有知识无法解决的难题。
初中常见的无理数有三种类型:
(1)含根号且开方开不尽的方根,但切不可认为带根号的数都是无理数;
(2)化简后含π的式子;
(3)不循环的无限小数。
掌握常见无理数的类型有助于识别无理数。
无理数的历史:
毕达哥拉斯(Pythagqras,约公元前885年至公元前400年间)是古希腊的大数学家。他证明许多重要的定理,包括后来以他的名字命名的毕达哥拉斯定理(勾股弦定理),即直角三角形两直角边为边长的正方形的面积之和等于以斜边为边长的正方形的面积。毕达哥拉斯将数学知识运用得纯熟之后,觉得不能只满足于用来算题解题,于是他试着从数学领域扩大到哲学,用数的观点去解释一下世界。经过一番刻苦实践,他提出“凡物皆数”的观点,数的元素就是万物的元素,世界是由数组成的,世界上的一切没有不可以用数来表示的,数本身就是世界的秩序。在他死后大约200年,他的门徒们把这种理论加以研究发展,形成了一个强大的毕达哥拉斯学派。
公元前500年,古希腊毕达哥拉斯(Pythagoras)学派的弟子希伯索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线与其一边的长度是不可公度的(若正方形的边长为1,则对角线的长不是一个有理数),这一不可公度性与毕氏学派的“万物皆数”(指有理数)的哲理大相径庭。这一发现使该学派领导人惶恐,认为这将动摇他们在学术界的统治地位,于是极力封锁该真理的流传,希伯索斯被迫流亡他乡,不幸的是,在一条海船上还是遇到毕氏门徒,于是希伯索斯被残忍地扔进了大海。
希伯索斯的发现,第一次向人们揭示了有理数系的缺陷,证明了它不能同连续的无限直线等同看待,有理数并没有布满数轴上的点,在数轴上存在着不能用有理数表示的“孔隙”。而这种“孔隙”经后人证明简直多得“不可胜数”。于是,古希腊人把有理数视为连续衔接的那种算术连续统的设想彻底地破灭了。不可公度量的发现连同芝诺悖论一同被称为数学史上的第一次数学危机,对以后2000多年数学的发展产生了深远的影响,促使人们从依靠直觉、经验而转向依靠证明,推动了公理几何学和逻辑学的发展,并且孕育了微积分思想萌芽。
不可约的本质是什么?长期以来众说纷纭,得不到正确的解释,两个不可通约的比值也一直认为是不可理喻的数。15世纪意大利著名画家达.芬奇称之为“无理的数”,17世纪德国天文学家开普勒称之为“不可名状”的数。
然而真理毕竟是淹没不了的,毕氏学派抹杀真理才是“无理”。人们为了纪念希伯索斯这位为真理而献身的可敬学者,就把不可通约的量取名“无理数”——这就是无理数的由来。
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。
矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形
矩形的判定:
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。
黄金矩形:
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。如希腊的巴特农神庙等。
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
特殊的长方形。
四条边都相等且四个角都是直角的四边形叫做正方形。
有一组邻边相等的矩形是正方形。
有一个角为直角的菱形是正方形。
对角线平分且相等,并且对角线互相垂直的四边形为正方形。
对角线相等的菱形是正方形。
正方形的性质:
1、边:两组对边分别平行;四条边都相等;相邻边互相垂直
2、内角:四个角都是90°;
3、对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;
4、对称性:既是中心对称图形,又是轴对称图形(有四条对称轴);
5、正方形具有平行四边形、菱形、矩形的一切性质;
6、特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;
正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
7、在正方形里面画一个最大的圆,该圆的面积约是正方形面积的78.5%;
正方形外接圆面积大约是正方形面积的157%。
8、正方形是特殊的长方形。
正方形的判定:
判定一个四边形为正方形的一般顺序如下:先证明它是平行四边形,再证明它是菱形(或矩形),最后证明它是矩形(或菱形)。
1:对角线相等的菱形是正方形。
2:有一个角为直角的菱形是正方形。
3:对角线互相垂直的矩形是正方形。
4:一组邻边相等的矩形是正方形。
5:一组邻边相等且有一个角是直角的平行四边形是正方形。
6:对角线互相垂直且相等的平行四边形是正方形。
7:对角线相等且互相垂直平分的四边形是正方形。
8:一组邻边相等,有三个角是直角的四边形是正方形。
9:既是菱形又是矩形的四边形是正方形。
有关计算公式:
若S为正方形的面积,C为正方形的周长,a为正方形的边长,则
正方形面积计算公式:S =a×a(即a的2次方或a的平方),或S=对角线×对角线÷2;
正方形周长计算公式: C=4a 。
S正方形= 。(正方形边长为a,对角线长为b)
。(正方形边长为a,对角线长为b)
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么说这两个图形关于这个点中心对称,这个点叫做对称中心。
中心对称图形的定义:
在平面内,一个图形绕着某一个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
中心对称的性质:
①关于中心对称的两个图形是全等形。
②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
③关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
中心对称的判定:
如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。
中心对称与中心对称图形的联系:
中心对称和中心对称图形是两个不同而又紧密联系的概念。
区别是:
中心对称是指两个全等图形之间的相互位置关系,这两个图形关于一点对称,这个点是对称中心,两个图形关于点的对称也叫做中心对称。成中心对称的两个图形中,其中一个图形上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点的对称点,又都在这个图形上;
而中心对称图形是指一个图形本身成中心对称。中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个中心对称图形,如果把对称的部分看成是两个图形,那么它们又是关于中心对称。
也就是说:
① 中心对称图形:如果把一个图形绕某一点旋转180度后能与自身重合,这个图形是中心对称图形。
②中心对称:如果把一个图形绕某一点旋转180度后能与另一个图形重合,这两个图形成中心对称。
如果两个图形形状相同,但大小不一定相等,那么称这两个图形相似。
相似比:
相似多边形对应边的比。
注:
(1)相似比是有顺序的;
(2)全等三角形是相似比为1的两个相似三角形。
主要性质:
1.对应内角相等
2.两个图形对应边成比例
如果是正方形,则只要边长成比例就可以,所以所有的正方形,正三角形都相似
长方形是长和高对应成比例
3.相似多边形的周长比等于相似比,面积比等于相似比的平方。
相似图形基本法则:
1. 如果选用同一个长度单位量得的两条线段AB,CD的长度分别是m,n那么就说这两条线段的比AB:CD=m:n,或写成AB/CD=m/n。
分别叫做这个线段比的前项后项。
2. 在地图或工程图纸上,图上长度与实际长度的比通常称为比例尺。
3. 四条线段a,b,c,d中,如果a与b的比等于c与d的比,即a/b=c/d,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
4. 如果a/b=c/d,那么ad=bc. 如果ad=bc(a,b,c,d都不等于0),那么a/b=c/d.
5. 如果a/b=c/d,那么(a±b)/b=(c±d)/d;那么(a±kb)/b=(c±kd)/d;那么a/b±ka=c/d±kc
6如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b.
7 如果AC/AB=BC/AC,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,(√5-1)/2叫做黄金比。
8. 长于宽的比等于黄金比的矩形叫做黄金矩形。
9. 三角形ABC与三角形A’B’C’是形状形同的图形,其中10 各角对应相等、各边对应成比例的两个多边形叫做<a>相似多边形。
11.相似多边形的比叫做相似比。
12.三角对应相等,三边对应成比例的两个三角形叫做相似三角形。若三角形ABC与三角形DEF相似,记作:
△ ABC∽△DEF,把对应顶点的字母写在相应的位置上
13.探索三角形相似的条件:
① 两角对应相等的两个三角形相似。
② 三边对应成比例的两个三角形相似。
③ 两边对应成比例且夹角相等的两个三角相似。
14.相似多边形的性质:
① 相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比。
② 相似多边形的周长比等于相似比,面积比等于相似比的平方(或相似比等于面积比的算术平方根)。
15.如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。
16.位似图形上任一对对应点到位似中心的距离之比和周长比等于位似比,且面积比等于位似比的平方
对应角相等,各边对应成比例的两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比。
17. 相似具有方向性与传递性。
18.位似是特殊的相似。
与“在下列说法中:(1)无限小数都是无理数;(2)如果将一个直...”考查相似的试题有:
- 在小学学了非负数,上初一引入了负数,数的范围扩充到有理数范围,那么引入无理数之后数的范围扩充到______范围.在实数3.14...
- 如图,在矩形ABCD中,O是对角线的交点,AE⊥BD于E,若OE:OD=1:2,AC=18cm,则AB=______cm.
- 如图,先把一个矩形纸片ABCD对折,设折痕为MN,再把点B叠在折痕MN上,得到△ABE,过点B折纸片使点D叠在直线AD上,得折痕PQ。(...
- 如图所示,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件 ,使四边形ABCD为矩形.
- (2011•北京)阅读下面材料:小伟遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积...
- 如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形。(1)求证:四边形ABCD是菱形;...
- (1)如图(1),△ABC为正三角形,点M是BC上任一点,点N是边AC上任一点,且BM=CN,直线AM与BN相交于点Q.∠BQM等于多少度?请...
- 如图,四边形ABCD是边长为2的正方形,以点A,B,C为圆心作圆,分别交BA,CB,DC的延长线于点E,F,G.(1)求点D沿三条圆弧运...
- 如图所示,P是边长为8的正方形ABCD形外一点,PB=PC,△PBD的面积等于48,求△PBC的面积.
- 在等边三角形、菱形、等腰梯形、平行四边形中,既是中心对称图形又是轴对称图形的是______.