本试题 “下列各式变形正确的是( )A.xy=x2xy2B.ba=b2a2C.yx=xyxD.a3•a-2=a” 主要考查您对有理数的乘方
零指数幂(负指数幂和指数为1)
分式的基本性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 有理数的乘方
- 零指数幂(负指数幂和指数为1)
- 分式的基本性质
有理数乘方的定义:
求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂。在an中,a叫做底数,n叫做指数。
22、73也可以看做是乘方运算的结果,这时它们表示数,分别读作“2的2次幂”、“7的3次幂”,其中2、7叫做底数,6、3叫做指数。
①习惯上把22叫做2的平方,把23叫做2的立方;
②当底数是负数或分数时,要先用括号将底数括上,再在其右上角写指数,指数要写得小些。
乘方的性质:
乘方是乘法的特例,其性质如下:
(1)正数的任何次幂都是正数;
(2)负数的偶次幂是正数,负数的奇次幂是负数;
(3)0的任何(除0以外)次幂都是0;
(4)a2是一个非负数,即a2≥0。
有理数乘方法则:
①负数的奇次幂是负数,负数的偶次幂是正数。例如:(-2)3=-8,(-2)2=4
②正数的任何次幂都是正数,0的任何正整数次幂都是0.例如:22=4,23=8,03=0
点拨:
①0的次幂没意义;
②任何有理数的偶次幂都是非负数;
③由于乘方是乘法的特例,因此有理数的乘方运算可以用有理数的乘法运算完成;
④负数的乘方与乘方的相反数不同。
乘方示意图:

求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂。在an中,a叫做底数,n叫做指数。
22、73也可以看做是乘方运算的结果,这时它们表示数,分别读作“2的2次幂”、“7的3次幂”,其中2、7叫做底数,6、3叫做指数。
①习惯上把22叫做2的平方,把23叫做2的立方;
②当底数是负数或分数时,要先用括号将底数括上,再在其右上角写指数,指数要写得小些。
乘方的性质:
乘方是乘法的特例,其性质如下:
(1)正数的任何次幂都是正数;
(2)负数的偶次幂是正数,负数的奇次幂是负数;
(3)0的任何(除0以外)次幂都是0;
(4)a2是一个非负数,即a2≥0。
有理数乘方法则:
①负数的奇次幂是负数,负数的偶次幂是正数。例如:(-2)3=-8,(-2)2=4
②正数的任何次幂都是正数,0的任何正整数次幂都是0.例如:22=4,23=8,03=0
点拨:
①0的次幂没意义;
②任何有理数的偶次幂都是非负数;
③由于乘方是乘法的特例,因此有理数的乘方运算可以用有理数的乘法运算完成;
④负数的乘方与乘方的相反数不同。
乘方示意图:

零指数幂定义:任何不等于零的数的零次幂都等于1。
负指数幂的定义:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数。
指数为1:任何不等于零的数的1次幂,所得结果都等于这个数的本身。
负指数幂的定义:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数。
指数为1:任何不等于零的数的1次幂,所得结果都等于这个数的本身。
分式的基本性质:
分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变。
即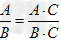 ,
,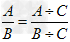 (C≠0),其中A、B、C均为整式。
(C≠0),其中A、B、C均为整式。
分式的符号法则:一个分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变。
约分:分数可以约分,分式与分数类似,也可以约分,根据分式的基本性质把一个分式的分子与分母的公因式约去,这种变形称为分式的约分。
分式的约分步骤:
(1)如果分式的分子和分母都是单项式或者是几个因式乘积的形式,将它们的公因式约去;
(2)分式的分子和分母都是多项式,将分子和分母分别分解因式,再将公因式约去。
通分:根据分式的基本性质,把分子、分母同时乘以适当的整式,把几个异分母的分式转化为与原来的分式相等的同分母的分式,叫做分式的通分。 分式的通分步骤:先求出所有分式分母的最简公分母,再将所有分式的分母变为最简公分母;同时各分式按照分母所扩大的倍数,相应扩大各自的分子.
分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变。
即
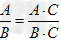 ,
,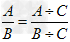 (C≠0),其中A、B、C均为整式。
(C≠0),其中A、B、C均为整式。 分式的符号法则:一个分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变。
约分:分数可以约分,分式与分数类似,也可以约分,根据分式的基本性质把一个分式的分子与分母的公因式约去,这种变形称为分式的约分。
分式的约分步骤:
(1)如果分式的分子和分母都是单项式或者是几个因式乘积的形式,将它们的公因式约去;
(2)分式的分子和分母都是多项式,将分子和分母分别分解因式,再将公因式约去。
通分:根据分式的基本性质,把分子、分母同时乘以适当的整式,把几个异分母的分式转化为与原来的分式相等的同分母的分式,叫做分式的通分。 分式的通分步骤:先求出所有分式分母的最简公分母,再将所有分式的分母变为最简公分母;同时各分式按照分母所扩大的倍数,相应扩大各自的分子.
发现相似题
与“下列各式变形正确的是( )A.xy=x2xy2B.ba=b2a2C.yx=xyxD...”考查相似的试题有:
- (﹣1)2009﹣(﹣1)2006=( ).
- 某种细胞开始有2个,1小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1个,…,按此规律,5小...
- 比较大小:-24______(-2)4,-25______(-2)5. (填“<”,“=”,“>”)
- 在2008年北京奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.581亿帕的钢材.4.58...
- 据人民网5月20日电报道:中国森林生态系统年涵养水源量约4948亿立方米,将4948亿用科学记数法表示为( )A.4.948×1013B.4.9...
- 下列说法正确的是( )A.零除以任何数都得0B.绝对值相等的两个数相等C.几个有理数相乘,积的符号由负因数的个数决定D.两...
- 下列运算中正确的是( )A.(6x6)÷(3x3)=2x2B.(8x8)÷(4x2)=2x6C.(3xy)2÷(3x)=yD.(x2y2)÷(xy)2=xy
- 计算:(-23)0+(13)-1÷3-|-3|.
- 计算下列各题:(1)12+(-2)2×4-1-4sin60°;(2)|-2|+(3)-1+20050.
- 下列运算正确的是( )A.x3+2x3=3x6B.2(a+b)=2a+bC.(1+2)(1-2)=1D.xy-2yx2-4x+4=yx-2