零指数幂定义：任何不等于零的数的零次幂都等于1。
负指数幂的定义：任何不等于零的数的-n（n为正整数）次幂，等于这个数的n次幂的倒数。
指数为1：任何不等于零的数的1次幂，所得结果都等于这个数的本身。
分式的加减乘除混合运算：
分式的混合运算应先乘方，再乘除，最后算加减，有括号的先算括号内的。也可以把除法转化为乘法，再运用乘法运算。
分式的化简：借助分式的基本性质，应用换元法、整体代入法等，通过约分和通分来达到简化分式的目的。
分式的混合运算：
在解答分式的乘除法混合运算时，注意两点，就可以了：
注意运算的顺序：按照从左到右的顺序依次计算；
注意分式乘除法法则的灵活应用。
二次根式:我们把形如
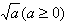
叫做二次根式。
二次根式必须满足：
含有二次根号“
”；
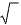
被开方数a必须是非负数。
确定二次根式中被开方数的取值范围：
要是二次根式
有意义，被开方数a必须是非负数，即a≥0，由此可确定被开方数中字母的取值范围。
二次根式性质：
（1）a≥0 ；
≥0 （双重非负性 )；
（2）
；
（3）
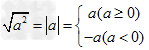0(a=0);
（4）
；
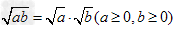
（5）
。
二次根式判定：
①二次根式必须有二次根号，如
，
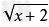等；
②二次根式中，被开方数a可以是具体的一个数，也可以是代数式；
③二次根式定义中a≥0 是定义组成的一部分,不能省略;
④二次根式是一个非负数;
⑤二次根式与算术平方根有着内在的联系,(a≥0 )就表示a的算术平方根。
二次根式的应用：
主要体现在两个方面：
（1）利用从特殊到一般，在由一般到特殊的重要思想方法，解决一些规律探索性问题；
（2）利用二次根式解决长度、高度计算问题，根据已知量，求出一些长度或高度，或设计省料的方案，以及图形的拼接、分割问题。这个过程需要用到二次根式的计算，其实就是化简求值。