本试题 “在直角坐标系xOy中，曲线C1的参数方程为x=cosαy=1+sinα（α为参数）在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，...” 主要考查您对简单曲线的极坐标方程
双曲线的参数方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 简单曲线的极坐标方程
- 双曲线的参数方程
曲线的极坐标方程的定义：
一般地，在极坐标系中，如果平面曲线C上任意一点的极坐标中至少有一个满足方程f（ρ，θ）=0，并且坐标适合方程f（ρ，θ）=0的点都在曲线上，那么方程f（ρ，θ）=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法：
直译法、待定系数法、相关点法等。
圆心为（α，β）（a＞0），半径为a的圆的极坐标方程为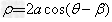
，此圆过极点O。
直线的极坐标方程：
直线的极坐标方程是ρ=1/（2cosθ＋4sinθ）。
圆的极坐标方程：
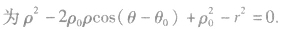
这是圆在极坐标系下的一般方程。
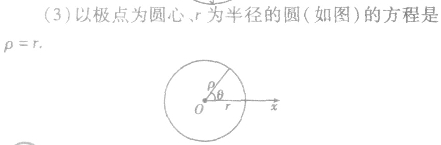
过极点且半径为r的圆方程：
双曲线的参数方程：
双曲线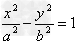
的参数方程是
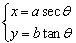（θ是参数，0≤θ＜2π，
）。
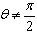双曲线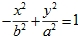
的参数方程是
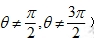
双曲线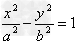上任意点M的坐标可设为
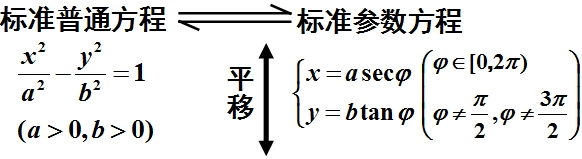
双曲线的普通方程和参数方程的关系:
发现相似题
与“在直角坐标系xOy中，曲线C1的参数方程为x=cosαy=1+sinα（α为...”考查相似的试题有：
- ⊙O1和⊙O2的极坐标方程分别为ρ=4cosθ，ρ=-4sinθ，则经过⊙O1，⊙O2交点的直线的直角坐标方程为（ ）。
- 极坐标方程（ρ-1）（θ-π）=0（ρ≥0）表示的图形是（ ）A.两个圆B.两条直线C.一个圆和一条射线D.一条直线和一条射线
- 选做题在直角坐标系xoy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为cos (θ－)=1，曲线C2的方程为.（θ...
- 极坐标系下，直线ρcos（θ-π4）=2与圆ρ=2的公共点个数是______．
- 若曲线的极坐标方程为，以极点为原点，极轴为x轴正半轴建立直角坐标系，则曲线的直角坐标方程为 .
- 在极坐标系中，曲线和的方程分别为和，以极点为平面直角坐标系的原点，极轴为轴正半轴，建立平面直角坐标系，则曲线和交点的...
- 在极坐标系中，曲线ρ=3截直线所得的弦长为（ ）。
- （坐标系与参数方程选做题）在极坐标系中，圆ρ=-2cosθ的圆心的极坐标是______．
- 看下图回答问题
- 在极坐标中，已知点为方程所表示的曲线上一动点，点的坐标为，则的最小值为____________.