本试题 ““利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,以满足市场需求,已知该厂家生产三种不同型号的手机,出厂价分别为甲种型号手机每部1800元,乙...” 主要考查您对二元一次方程组的应用
三元(及三元以上)一次方程(组)的解法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二元一次方程组的应用
- 三元(及三元以上)一次方程(组)的解法
1. 行程问题(匀速运动)
基本关系:s=vt
①相遇问题(同时出发):
确定行程过程中的位置路程
相遇路程÷速度和=相遇时间
相遇路程÷相遇时间= 速度和
相遇问题(直线)
甲的路程+乙的路程=总路程
相遇问题(环形)
甲的路程 +乙的路程=环形周长
②追及问题(同时出发):
追及时间=路程差÷速度差
速度差=路程差÷追及时间
追及时间×速度差=路程差
追及问题(直线)
距离差=追者路程-被追者路程=速度差X追及时间
追及问题(环形)
快的路程-慢的路程=曲线的周长
③水中航行
顺水行程=(船速+水速)×顺水时间
逆水行程=(船速-水速)×逆水时间
顺水速度=船速+水速
逆水速度=船速-水速
静水速度=(顺水速度+逆水速度)÷2
水速:(顺水速度-逆水速度)÷2
2.配料问题:溶质=溶液×浓度
溶液=溶质+溶剂
3.增长率问题
4.工程问题
基本关系:工作量=工作效率×工作时间(常把工作量看成单位“1”)。
5.几何问题
①常用勾股定理,几何体的面积、体积公式,相似形及有关比例性质等。
②注意语言与解析式的互化:
如,“多”、“少”、“增加了”、“增加为(到)”、“同时”、“扩大为(到)”、“扩大了”、……
又如,一个三位数,百位数字为a,十位数字为b,个位数字为c,则这个三位数为:100a+10b+c,而不是abc。
③注意从语言叙述中写出相等关系:
如,x比y大3,则x-y=3或x=y+3或x-3=y。又如,x与y的差为3,则x-y=3。
④注意单位换算:
如,“小时”“分钟”的换算;s、v、t单位的一致等。
二元一次方程组的应用:
列方程(组)解应用题是中学数学联系实际的一个重要方面。
其具体步骤是:
⑴审题。理解题意。弄清问题中已知量是什么,未知量是什么,问题给出和涉及的相等关系是什么。
⑵设元(未知数)。①直接未知数②间接未知数(往往二者兼用)。一般来说,未知数越多,方程越易列,但越难解。
⑶用含未知数的代数式表示相关的量。
⑷寻找相等关系(有的由题目给出,有的由该问题所涉及的等量关系给出),列方程。一般地,未知数个数与方程个数是相同的。
⑸解方程及检验。
⑹答案。
综上所述,列方程(组)解应用题实质是先把实际问题转化为数学问题(设元、列方程),在由数学问题的解决而导致实际问题的解决(列方程、写出答案)。在这个过程中,列方程起着承前启后的作用。因此,列方程是解应用题的关键。
三元一次方程的定义:
就是含有三个未知数,并且含有未知数的项的次数是1的整式方程。如x+y-z=1,2a-3b+c=0等都是三元一次方程。
三元一次方程组:
方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,这样的方程组叫做三元一次方程组。
例如: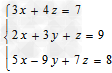 就是三元一次方程组。
就是三元一次方程组。
注:三元一次方程组必须满足:
1.方程组中有且只有三个未知数;
2.含未知数的项的次数都是1.
3.每个方程中不一定都含有三个未知数。
三元一次方程(组)的解:
一般的,使三元一次方程等号两边的值相等的三个未知数的值,叫作三元一次方程的解。
三元一次方程组的三个方程的公共解,叫作三元一次方程的解。
三元一次方程组的解题思路及步骤:
思路:
通过“代入”或“加减”进行消元,把“三元”转化为“二元”,即准化为解二元一次方程组,进而再转化为解一元一次方程。
解三元一次方程组的基本思想仍是消元,其基本方法是代入法和加减法.
类型:
类型一:有表达式,用代入法;
类型二:缺某元,消某元。还可以通过消掉未知项y来达到将“三元”转化为“二元”目的。
步骤:
①利用代入法或加减法,消去一个未知数,得出一个二元一次方程组;
②解这个二元一次方程组,求得两个未知数的值;
③将这两个未知数的值代入原方程中较简单的一个方程,求出第三个未知数的值,把这三个数写在一起的就是所求的三元一次方程组的解。
注意:
①要根据方程的特点决定首先消去哪个未知数;
②原方程组的每个方程在求解过程中至少要用到一次;
③将所求得的一组未知数的值分别代入原方程组的每一个方程中进行检验,看每个方程等号左右两边的值是否相等,若都相等,则是原方程组的解,只要有一个方程等号左右两边的值不相等就不是原方程组的解。
例:
解方程组: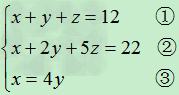
发现三个方程中x的系数都是1,因此确定用减法“消x”.
解法1:消x
②-① 得 y+4z=10 .④
③代人① 得5y+z=12 . ⑤
由④、⑤解得: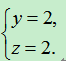
把y=2,代入③,得x=8.
∴ 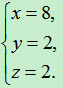 是原方程组的解.
是原方程组的解.
方程③是关于x的表达式,确定“消x”的目标。
解法2:消x
由③代入①②得
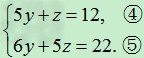
解得: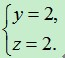
把y=2代入③,得x=8.
∴ 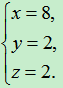 是原方程组的解。
是原方程组的解。
与““利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机...”考查相似的试题有:
- 一个长方形周长是16cm,长与宽的差是1cm,那么长与宽分别为( )A.3cm,5cmB.3.5cm,4.5cmC.4cm,6cmD.10cm,6cm
- 、如图,8块相同的长方形地砖拼成一个长方形,每块长方形地砖的长和宽分别是多少?现在请你设未知数列方程组来解决这个问题.
- 已知方程,用的代数式表示为 .
- 已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组的解是________.
- 某商场用36000元购进A、B两种商品,销售完后共获利6000元,其进价和售价如右表:(1) 该商场购进A、B两种商品各多少件?(2...
- (10分)某商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售工艺品8件时,与将标价降低35元销售该工艺品12件所...
- 某一组同学分一批练习本,若每人分6本,则少6本;若每人分5本,则多5本,若设x个同学,y本练习本,则得到的方程组是______.
- 已知a+b=3,2b-c=2,则2a+c=______.
- 已知方程组y2=nxy=2x+m(其中m、n均为不为零的常数)有一组实数解(1)确定mn的值;(2)若已知n=4,试解这个方程组.
- 解方程组:(1)x2-y+13=13(x-1+2y=13(2)2a+b+c=04a+2b+c=52a-b+c=4