本试题 “下列运算中,正确的是[ ]A、B、x6÷x3=x2C、2-1=-2D、a3·(-a2)=-a5” 主要考查您对零指数幂(负指数幂和指数为1)
整式的乘法
整式的除法
二次根式的加减
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 零指数幂(负指数幂和指数为1)
- 整式的乘法
- 整式的除法
- 二次根式的加减
零指数幂定义:任何不等于零的数的零次幂都等于1。
负指数幂的定义:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数。
指数为1:任何不等于零的数的1次幂,所得结果都等于这个数的本身。
负指数幂的定义:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数。
指数为1:任何不等于零的数的1次幂,所得结果都等于这个数的本身。
单项式和多项式都统称为整式。整式是有理式的一部分,在有理式中可以包含加,减,乘,除、乘方五种运算,但在整式中除数不能含有字母。把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个多项式因式分解(也叫作分解因式)。分解因式与整式乘法互逆。
1、单项式与单项式相乘的法则
单项式和单项式相乘,只要将它们的系数,相同字母的幂分别相乘,对于只在一个单项式中出项的字母,则连同它的指数一起作为积的一个因式.注意:单项式与单项式相乘的法则也适用于多个单项式相乘.
2.单项式与多项式相乘的法则
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.即m(a+b+c)=ma+mb+mc
3.多项式与多项式相乘的法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.即(m+n)*(a+b)=ma+mb+na+nb
整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除数不能含有字母。单项式和多项式统称为整式。单项式相除,把它们的系数相除,同底数幂的幂相减,作为商的一个因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。 单项式除以多项式,用单项式除以多项式的每一项,再将所得的商相加并合并同类项。
整式的除法法则:
1、同底数的幂相除:法则:同底数的幂相除,底数不变,指数相减。
数学符号表示: 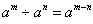 (a≠0,m、n为正整数,并且m>n)
(a≠0,m、n为正整数,并且m>n)
2、两个单项式相除,把系数、同底数幂分别相除后,作为商的因式;
对于只在被除式里含有的字母,则连同他的指数一起作为商的一个因式。
3、多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加。
整式的除法运算:
单项式÷单项式
单项式相除,把系数、同底数幂分别相除后,作为商的因式;
对于只在被除式中含有的字母,则连同它的指数一起作为商的一个因式。
注:单项式除以单项式主要是通过转化为同底数幂的除法解决的。
多项式÷单项式
多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加。
说明:多项式(没有同类项)除以单项式,结果的项数与多项式的项数相同,不要漏项。
多项式÷单项式
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
单项式除以多项式,用单项式除以多项式的每一项,再将所得的商相加并合并同类项。
二次根式加减法法则:
先把式子中各项二次根式化成最简二次根式,然后再合并同类二次根式。
1、同类二次根式
一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式。
2、合并同类二次根式
把几个同类二次根式合并为一个二次根式就叫做合并同类二次根式。
3、二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的进行合并。
例如:(1);2 +3
+3 =5
=5 (2)
(2)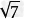 +2
+2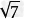 =3
=3
4、注意:有括号时,要先去括号。
二次根式的加减注意:
①二次根式合并同类项与合并同类项类似,因此二次根式的加减可以对比整式的加减进行;
②二次根式加减混合运算的是指就是合并同类项二次根式,不是同类二次根式不能合并。如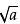 +
+ 是最简结果,不能再合并;
是最简结果,不能再合并;
③二次根式进行加减运算时,根号外的系数因式须保留假分数形式,如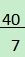
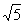 ,不能写成5
,不能写成5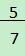
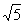
④合并同类二次根式后若系数为多项式,须添加括号。
先把式子中各项二次根式化成最简二次根式,然后再合并同类二次根式。
1、同类二次根式
一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式。
2、合并同类二次根式
把几个同类二次根式合并为一个二次根式就叫做合并同类二次根式。
3、二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的进行合并。
例如:(1);2
 +3
+3 =5
=5 (2)
(2)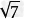 +2
+2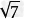 =3
=3
4、注意:有括号时,要先去括号。
二次根式的加减注意:
①二次根式合并同类项与合并同类项类似,因此二次根式的加减可以对比整式的加减进行;
②二次根式加减混合运算的是指就是合并同类项二次根式,不是同类二次根式不能合并。如
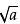 +
+ 是最简结果,不能再合并;
是最简结果,不能再合并;③二次根式进行加减运算时,根号外的系数因式须保留假分数形式,如
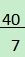
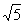 ,不能写成5
,不能写成5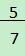
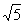
④合并同类二次根式后若系数为多项式,须添加括号。
发现相似题
与“下列运算中,正确的是[ ]A、B、x6÷x3=x2C、2-1=-2D、a3·(-a2...”考查相似的试题有:
- 计算:(1)(2-3)0-(12)-2+(14)2011×(-4)2011(2)2(a4)3+(-2a3)2-(-a2)3+a2a10(3)(-2x2y)3+(x2)2-[(-3x)2-y3-...
- 计算(π-2)0+(13)-1-27cos30°
- 计算:4-(π-3)0-10sin30°-(-1)2013+(13)-2.
- 计算:(π+1)0-12+|-3|.
- 下列计算正确的是( )A.B.C.D.
- (5分)请把下面不完整的数轴画完整,并在数轴上标出下列各数:-3,,4
- 下列各式由左边到右边的变形中,是因式分解的为 A.m(x+y)=mx+myB.8x2-4x=4x(2x-1)C.x2-6x+5=x(x-6)+5D.x2-9...
- 计算(1)(2)(精确到0.01)
- 计算:;
- 阅读下面材料,并解答后面的问题:;;.(1)观察上面的等式,请直接写出的结果 ;(2)计算= ,此时称与互为有理化因式;(3...