本试题 “有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定.大桥上的车距d(m)与车速v(km/h)和车长l(m)的关系满足:d=kv2l+12l(k为...” 主要考查您对指数函数模型的应用
对数函数模型的应用
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数函数模型的应用
- 对数函数模型的应用
- 基本不等式及其应用
恰当选择自变量将问题的目标表示成自变量的函数f(x)=a·bx+c(a、b、c为常数,a≠0,b>0,b≠1)的形式,进而结合指数函数的性质解决问题。
指数型复合函数的性质的应用:
(1)与指数函数有关的复合函数基本上有两类:![]() ;②
;②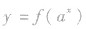 .无论是哪一类,要搞清楚复合过程,才能确定复合函数的值域和单调区间,具体问题中,a的取值不定时,要对a进行分类讨论.
.无论是哪一类,要搞清楚复合过程,才能确定复合函数的值域和单调区间,具体问题中,a的取值不定时,要对a进行分类讨论.
(2)对于形如![]() 一类的指数型复合函数,有以下结论:
一类的指数型复合函数,有以下结论:
①函数 的定义域与f(x)的定义域相同;
的定义域与f(x)的定义域相同;
②先确定函数f(x)的值域,再根据指数函数的值域、单调性,确定函数 的值域;
的值域;
③当a>l时,函数 与函数f(x)的单调性相同;当O<a<l时,函数
与函数f(x)的单调性相同;当O<a<l时,函数 与函数f(x)的单调性相反.
与函数f(x)的单调性相反.
对数函数模型的定义:
恰当选择自变量将问题的目标表示成自变量的函数f(x)=mlogax+n(m、n、a为常数,m≠0,a>0,a≠1)的形式,进而结合对数函数的性质解决问题。
对数函数模型解析式:
f(x)=mlogax+n(m、n、a为常数,m≠0,a>0,a≠1)
用函数模型解函数应用题的步骤:
1.审题:弄清题意,分清条件和结论,确定数量关系,初步选择数学模型;
2.建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;
3.求模:求解数学模型,得出数学结论;
4.还原:将数学问题还原为实际问题的意义。
基本不等式:
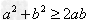 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①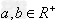 ,
,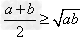 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②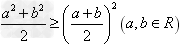 ;③
;③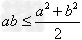 ;④
;④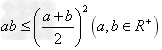 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有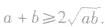
(2)基本不等式又称为均值定理、均值不等式等,其中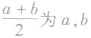 的算术平均数,
的算术平均数,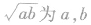 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即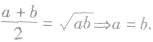
对于两个正数x,y,若已知xy,x+y,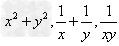 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2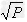 ,
,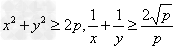 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值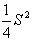 ,
,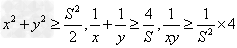 ;
;
(3)已知x2+y2=p,则x+y有最大值为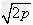 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式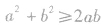 的形式可以是
的形式可以是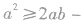
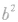 ,也可以是
,也可以是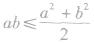 ,还可以是
,还可以是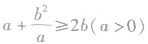 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

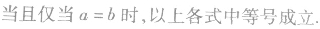
与“有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安...”考查相似的试题有:
- 如图半径为2的圆内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.(1)写出这个梯形周长y和腰长x间的函数式...
- 看下图回答问题
- 已知函数,. (1)求函数的定义域;(2)当时,总有成立,求的取值范围.
- 若实数a,b满足a2+b2=6,则ab的最大值为______.
- 若x>0,则函数y=1+x+4x的最小值为( )A.3B.334C.5D.6
- A杯中有浓度为a%的盐水x克,B杯中有浓度为b%的盐水y克,其中A杯中的盐水更咸一些.若将A、B两杯盐水混合在一起,其咸淡的程度...
- 已知a,b,c∈R+,求证:≥a+b+c。
- 已知正数满足,则的最小值为 .
- 已知a,b,c是不全相等的正数,求证:(ab+a+b+1)(ab+ac+bc+c2)>16abc.
- 若x+2y=4,则2x+4y的最小值是______.