本试题 “已知a<b,则有以下结论①a+c<b+c;②;③c﹣a>c﹣b;④a|c|<b|c|,其中正确的结论的序号是[ ]A.①③B.①②③C.①③④D.①②③④” 主要考查您对不等式的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 不等式的性质
不等式的性质:
1、不等式的基本性质:
不等式性质1:不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变。即如果a>b,那么a±c>b±c。
不等式性质2:不等式的两边同时乘(或除以)同一个正数,不等号的方向不变。即如果a>b,c>0,那么ac>bc(或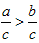 )。
)。
不等式性质3:不等式的两边同时乘(或除以)同一个负数,不等号的方向改变。即如果a>b,c<0,那么ac<bc(或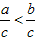 )。
)。
2、不等式的互逆性:若a>b,则b<a。
3、不等式的传递性:若a>b,b>c,则a>c。
不等式的基本性质和等式的基本性质的异同:
①相同点:无论是等式还是不等式,都可以在它的两边加(或减)同一个数或同一个整式;
②不同点:对于等式来说,在等式的两边乘(或除以)同一个正数(或同一个负数),等式仍然成立,但是对于不等式来说,却不大一样,在不等式的两边乘(或除以)同一个正数,不等号的方向不变,而在不等式的两边乘(或除以)同一个负数,不等号要改变方向。
1、不等式的基本性质:
不等式性质1:不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变。即如果a>b,那么a±c>b±c。
不等式性质2:不等式的两边同时乘(或除以)同一个正数,不等号的方向不变。即如果a>b,c>0,那么ac>bc(或
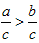 )。
)。不等式性质3:不等式的两边同时乘(或除以)同一个负数,不等号的方向改变。即如果a>b,c<0,那么ac<bc(或
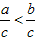 )。
)。2、不等式的互逆性:若a>b,则b<a。
3、不等式的传递性:若a>b,b>c,则a>c。
不等式的性质:
①如果x>y,那么y<x;如果y<x,那么x>y;(对称性)
②如果x>y,y>z;那么x>z;(传递性)
③如果x>y,而z为任意实数或整式,那么x+z>y+z;(加法原则,或叫同向不等式可加性)
④ 如果x>y,z>0,那么xz>yz;如果x>y,z<0,那么xz<yz;(乘法原则)
⑤如果x>y,z>0,那么x÷z>y÷z;如果x>y,z<0,那么x÷z<y÷z;
⑥如果x>y,m>n,那么x+m>y+n;(充分不必要条件)
⑦如果x>y>0,m>n>0,那么xm>yn;
⑧如果x>y>0,那么x的n次幂>y的n次幂(n为正数),x的n次幂<y的n次幂(n为负数)
或者说,不等式的基本性质有:
①对称性;
②传递性:
③加法单调性:即同向不等式可加性:
④乘法单调性:
⑤同向正值不等式可乘性:
⑥正值不等式可乘方:
⑦正值不等式可开方:
⑧倒数法则。
不等式的基本性质和等式的基本性质的异同:
①相同点:无论是等式还是不等式,都可以在它的两边加(或减)同一个数或同一个整式;
②不同点:对于等式来说,在等式的两边乘(或除以)同一个正数(或同一个负数),等式仍然成立,但是对于不等式来说,却不大一样,在不等式的两边乘(或除以)同一个正数,不等号的方向不变,而在不等式的两边乘(或除以)同一个负数,不等号要改变方向。
原理:
①不等式F(x)< G(x)与不等式 G(x)>F(x)同解。
②如果不等式F(x) < G(x)的定义域被解析式H( x )的定义域所包含,那么不等式 F(x)<G(x)与不等式F(x)+H(x)<G(x)+H(x)同解。
③如果不等式F(x)<G(x) 的定义域被解析式H(x)的定义域所包含,并且H(x)>0,那么不等式F(x)<G(x)与不等式H(x)F(x)<H( x )G(x) 同解;如果H(x)<0,那么不等式F(x)<G(x)与不等式H (x)F(x)>H(x)G(x)同解。
④不等式F(x)G(x)>0与不等式同解;不等式F(x)G(x)<0与不等式同解。
发现相似题
与“已知a<b,则有以下结论①a+c<b+c;②;③c﹣a>c﹣b;④a|c|<b...”考查相似的试题有:
- 如果a<0,b>0,a+b<0,那么下列关系式中正确的是[ ]A.a>b>﹣b>﹣aB.a>﹣a>b>﹣bC.b>a>﹣b>﹣aD.﹣a>b>﹣b>a
- 设a、b、c均为正数,若,则a、b、c三个数的大小关系是[ ]A.c<a<bB.b<c<aC.a<b<cD.c<b<a
- 若m<n,比较下列各式的大小:(1)m-3______n-3 (2)-5m______-5n (3)-m3______-n3(4)3-m______2-n (5)0______m-n (...
- 看下图回答问题
- 不等式2x-4>0的解集是________________
- 一商场计划到计算器生产厂家购进一批A、B两种型号的计算器。经过商谈,A型计算器单价为50元,100只起售,超过100只的超过部分...
- 不等式组的解集在数轴上表示正确的是( ).A.B.C.D.
- 若a>b,则 ( )A.a>-bB.a-2bD.-2a
- 当x取何值时,代数式与的值的差大于4?
- 如果x>y,那么下列结论中错误的是[ ]A.3x>3yB.x-3>y-3C.D.-x-3>-y-3