本试题 “已知正方形ABCD的边长为2,E、F、G、H分别是边AB、BC、CD、DA的中点.(1)在正方形ABCD内部随机取一点P,求满足|PH|<2的概率;(2)从A、B、C、D、E、F、G...” 主要考查您对几何概型的定义及计算
离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 几何概型的定义及计算
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
几何概型的概念:
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)称比例,则称这样的概率模型为几何概率模型,简称为几何概型。
几何概型的概率:
一般地,在几何区域D中随机地取一点,记事件"该点落在其内部一个区域d内"为事件A,则事件A发生的概率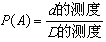 。
。
说明:(1)D的测度不为0;
(2)其中"测度"的意义依D确定,当D分别是线段,平面图形,立体图形时,相应的"测度"分别是长度,面积和体积;
(3)区域为"开区域";
(4)区域D内随机取点是指:该点落在区域内任何一处都是等可能的,落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关.
几何概型的基本特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等.
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称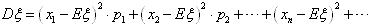 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,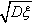 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)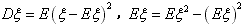 ;
;
(2)若η=aξ+b,则 ;
;
(3)若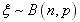 ,则
,则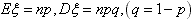 ;
;
(4)若ξ服从几何分布,则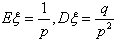 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式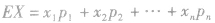 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“已知正方形ABCD的边长为2,E、F、G、H分别是边AB、BC、CD、DA...”考查相似的试题有:
- 在1,2,3,4,5这五个数中,任取两个不同的数记作a,b,则满足f(x)=x2-ax+b有两个零点的概率是( )。
- 在区间上随机取一个数,则的值介于到的概率是
- 若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现.试求方程x2+2px-q2+1=0有两个实数根的概率.
- 已知随机变量Z服从正态分布N(0,),若P(Z>2)=0.023,则P(-2≤Z≤2)=
- (本小题满分13分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试。在待测试的某一个小...
- 今有4种股票和3种基金,李先生欲购买其中的任意3种产品.(1)求李先生所购买的3种产品中恰好只含一种基金的概率;(2)记购...
- 设l为平面上过点(0,1)的直线,l的斜率等可能地取-22,-3,-52,0,52,3,22,用X表示坐标原点到l的距离,则随机变量ξ的数...
- 小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只...
- 深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球)....
- 随机变量的分布列如下图所示 ,则E(5 ξ+4)等于 ξ 0 2 4 P 0.4 0.3 0.3 A.13B.11C.2.2D.1.8