本试题 “在长度分别为3cm,4cm,5cm,7cm的四条线段中,随机取出三条,能构成三角形的概率是( )A.14B.34C.12D.1” 主要考查您对概率的意义
三角形的三边关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 概率的意义
- 三角形的三边关系
概率的意义:
一般地,在大量重复试验中,如果事件A发生的频率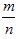 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤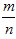 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;
(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
一般地,在大量重复试验中,如果事件A发生的频率
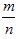 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤
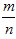 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
三角形的三边关系:
在三角形中,任意两边和大于第三边,任意两边差小于第三边。
设三角形三边为a,b,c
则
a+b>c
a+c>b
b+c>a
a-b<c
a-c<b
b-c<a
在直角三角形中,设a、b为直角边,c为斜边。
则两直角边的平方和等于斜边平方。
在等边三角形中,a=b=c
在等腰三角形中, a,b为两腰,则a=b
在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下,c2=a2+b2-2abcosc
三角形的三边关系定理及推论:
(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:
①判断三条已知线段能否组成三角形;
②当已知两边时,可确定第三边的范围;
③证明线段不等关系。
发现相似题
与“在长度分别为3cm,4cm,5cm,7cm的四条线段中,随机取出三条...”考查相似的试题有:
- 从1到9这9个自然数中任取一个,是2的倍数或是3的倍数的概率是( )A.19B.29C.23D.59
- 在两个袋子中分别装有大小、质地完全相同的的卡片. 甲袋中放了3张卡片,卡片上的数字分别为1,2,3;乙袋中放了2张卡片,卡...
- 一个不透明的袋子里装有除颜色外完全相同的2个红球和3个黄球,从袋子里任意摸出一个球是红球的概率为_________.
- 学校评选出30名优秀学生,要选5名代表参加全市优秀学生表彰会,已经确定了1名代表,则剩余学生参加全市优秀学生表彰会的概率...
- 以下说法正确的是( )A.在同一年出生的400人中至少有两人的生日相同B.一个游戏的中奖率是1%,买100张奖券,一定会中奖C....
- 小刚掷一枚均匀的硬币,一连99次都掷出正面朝上,当他第100次掷硬币时,出现正面朝上的概率是[ ]A.0B.1C.D.
- 下列说法正确的是[ ]A.“明天的降水概率为30%”是指明天下雨的可能性是30%B.连续抛一枚硬币50次,出现正面朝上的次数一定是25...
- 布袋中装有3个黑球和m个白球,它们除颜色不相同外,其余都相同,小明通过实验发现,随机从布袋中摸出一球是黑球的概率是14,...
- 如图2中每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖标志,则随机翻动一块木牌中奖的概率为A.B...
- 已知△ABC三边长分别为a,b,c,若|bc-2a|+(b+c-5)2=0,求b的取值范围。