本试题 “(1)已知方程的解是关于x的方程2k﹣x﹣k(x+4)=5的解,求k的值.(2)在(1)的条件下,已知线段AB=12cm,点C是直线AB上一点,且AC:BC=1:k,若点D是AC的...” 主要考查您对一元一次方程的解法
直线,线段,射线
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一元一次方程的解法
- 直线,线段,射线
使方程左右两边相等的未知数的值叫做方程的解。
解一元一次方程的注意事项:
1、分母是小数时,根据分数的基本性质,把分母转化为整数;
2、去分母时,方程两边各项都乘各分母的最小公倍数,此时不含分母的项切勿漏乘,分数线相当于括号,去分母后分子各项应加括号;
3、去括号时,不要漏乘括号内的项,不要弄错符号;
4、移项时,切记要变号,不要丢项,有时先合并再移项,以免丢项;
5、系数化为1时,方程两边同乘以系数的倒数或同除以系数,不要弄错符号;
6、不要生搬硬套解方程的步骤,具体问题具体分析,找到最佳解法;
7、分、小数运算时不能嫌麻烦;
8、不要跳步,一步步仔细算 。
解一元一次方程的步骤:
一般解法:
⒈去分母:在方程两边都乘以各分母的最小公倍数(不含分母的项也要乘);
依据:等式的性质2
⒉ 去括号:一般先去小括号,再去中括号,最后去大括号,可根据 乘法分配律(记住如括号外有减号或除号的话一定要变号)
依据:乘法分配律
⒊ 移项:把方程中含有 未知数的项都移到方程的一边(一般是含有未知数的项移到方程左边,而把常数项移到右边)
依据:等式的性质1
⒋ 合并同类项:把方程化成ax=b(a≠0)的形式;
依据:乘法分配律(逆用乘法分配律)
⒌ 系数化为1:在方程两边都除以未知数的系数a,得到方程的解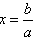
依据:等式的性质2
方程的同解原理 :
如果两个方程的解相同,那么这两个方程叫做同解方程。
⒈方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程。
⒉方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程。
做一元一次方程应用题的重要方法:
⒈认真 审题(审题)
⒉分析已知和未知量
⒊找一个合适的 等量关系
⒋设一个恰当的未知数
⒌列出合理的方程 (列式)
⒍解出方程(解题)
⒎ 检验
⒏写出答案(作答)
例:ax=b(a、b为常数)?
解:当a≠0,b=0时,
ax=0
x=0(此种情况与下一种一样)
当a≠0时,x=b/a。
当a=0,b=0时,方程有无数个解(注意:这种情况不属于一元一次方程,而属于恒等方程)
当a=0,b≠0时,方程无解(此种情况也不属于一元一次方程)
例:
(3x+1)/2-2=(3x-2)/10-(2x+3)/5
去分母(方程两边同乘各分母的最小 公倍数)得:
5(3x+1)-10×2=(3x-2)-2(2x+3)
去括号得:
15x+5-20=3x-2-4x-6
移项得:
15x-3x+4x=-2-6-5+20
合并同类项得:
16x=7
系数化为1得:
x=7/16。
注:字母公式(等式的性质)
a=b a+c=b+c a-c=b-c (等式的性质1)
a=b ac=bc
a=bc(c≠0)= a÷c=b÷c(等式的性质2)
检验 算出后需检验的。
求根公式
由于一元一次方程是 基本方程,教科书上的解法只有上述的方法。
但对于标准形式下的一元一次方程 ax+b=0
可得出求根公式x=-(b/a)
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意:
①线和射线无长度,线段有长度。
②直线无端点,射线有一个端点,线段有两个端点。
直线、射线、线段的基本性质:
| 图形 | 表示法 | 端点 | 延长线 | 能否度量 | 基本性质 | |
| 直线 | 没有端点的一条线 | 一条线, 不要端点 |
无 | 可以向两边无限延长 | 否 | 两端都没有端点,可以无限延长,不可测量的线 |
| 射线 | 只有一个端点的一条线 | 一条线, 只有一边有端点 |
一个 | 可以向一边无限延长 | 否 | 一端有端点,可以向一边无限延长,不可测量的线 |
| 线段 | 两边都有端点的一条线 | 一条线,两边都有端点 | 两个 | 不能延长 | 能 | 两端都有端点,不能延长,可测量的线 |
直线、射线、线段区别:
直线没有端点,2边可无限延长;
射线有1端有端点,另一端可无限延长;
线段,有2个端点,而2个端点间的距离就是这条线段的长度。
直线除了“直”这个特点外,还有一个很重要的特点,那就是它可以向两个方向无限延伸,永远没有尽头,所以,直线是不可能度量的。因此,在画直线时,要画出没有端点的直线,表示可以无限延伸;
射线只有一个端点,可以向一个方向无限延伸,也永远没有尽头。所以,射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线,因此,射线是直线的一部分。虽然射线是直线的一部分,但由于它们都是不能度量的,所以,它们之间没有长短可以比较;
线段有两个端点,它有一定的长度,可以度量。线段也是直线的一部分。
各种图形表示方法:
直线:一个小写字母或两个大写字母,但前面必须加“直线”两字,如:直线l,直线m;直线AB,直线CD。
例:
 直线l;直线AB。
直线l;直线AB。射线:一个小写字母或端点的大写字母。和射线上的一个大写字母,前面必须加“射线”两字。如:射线a;射线OA。
例:
 射线AB。
射线AB。线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a。
例:
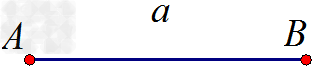 线段AB;线段a 。
线段AB;线段a 。与“(1)已知方程的解是关于x的方程2k﹣x﹣k(x+4)=5的解,求k...”考查相似的试题有:
- 图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是 cm3.
- 解下列方程:(1)3x-1x-2=0(2)x-2x+2-1=16x2-4.
- 某商品的原价为a元,提价10%后发现销售量锐减,欲恢复原价出售,则应约降价A.10%B.9%C.9.1%D.11.3%
- 小李在解方程5a-x=13(x为未知数)时,误将-x看作+x,得方程的解为x=-2,则原方程的解为( )A.x=0B.x=1C.x=2D.x=3
- 下列方程是一元一次方程的是 A.=5xB.x+1=3xC.y+y=0D.2x-3y=1
- 当x=4时,式子5(x+b)-10与bx+4x的值相等,则b=______.
- 下列说法正确的是( )A.直线AB和直线BA是两条直线B.射线AB和射线BA是两条射线C.线段AB和线段BA是两条线段D.直线AB和直线...
- 如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6...
- 如图,AB=6cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度。
- 如图,从A地到B地有3条路线可供选择,从B地到C地有2条路线可供选择,则从A地到C地可供选择的方案有______种.