本试题 “某校要组建篮球队,需要在各班选拔预备队员,规定投篮成绩一级的可作为入围选手,选拔过程中每人最多投篮5次,且规定在确认已经入围后则不必再投篮.若投中2...” 主要考查您对随机事件及其概率
条件概率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 随机事件及其概率
- 条件概率
随机事件的定义:
在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,随机事件通常用大写英文字母A、B、C等表示。
必然事件的定义:
必然会发生的事件叫做必然事件;
不可能事件:
肯定不会发生的事件叫做不可能事件;
概率的定义:
在大量进行重复试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
m,n的意义:事件A在n次试验中发生了m次。
因0≤m≤n,所以,0≤P(A)≤1,必然事件的概率为1,不可能发生的事件的概率0。
随机事件概率的定义:
对于给定的随机事件A,随着试验次数的增加,事件A发生的频率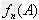 总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
频率的稳定性:
即大量重复试验时,任何结果(事件)出现的频率尽管是随机的,却“稳定”在某一个常数附近,试验的次数越多,频率与这个常数的偏差大的可能性越小,这一常数就成为该事件的概率;
“频率”和“概率”这两个概念的区别是:
频率具有随机性,它反映的是某一随机事件出现的频繁程度,它反映的是随机事件出现的可能性;概率是一个客观常数,它反映了随机事件的属性。
条件概率的定义:
(1)条件概率的定义:对于任何两个事件A和B,在已知事件A发生的条件下,事件B发生的概率叫做条件概率,用符号P(B|A)来表示.
(2)条件概率公式: 称为事件A与B的交(或积).
称为事件A与B的交(或积).
(3)条件概率的求法:
①利用条件概率公式,分别求出P(A)和P(A∩B),得P(B|A)=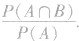
②借助古典概型概率公式,先求出事件A包含的基本事件数n(A),再在事件A发生的条件下求出事件B包含的基本事件数,即n(A∩B),得P(B|A)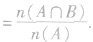
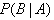 的性质:
的性质:
(1)非负性:对任意的A∈Ω,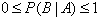 ;
;
(2)规范性:P(Ω|B)=1;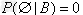
(3)可列可加性:如果是两个互斥事件,则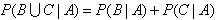 。
。
概率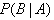 和P(AB)的区别与联系:
和P(AB)的区别与联系:
(1)联系:事件A和B都发生了;
(2)区别:a、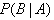 中,事件A和B发生有时间差异,A先B后;在P(AB)中,事件A、B同时发生。
中,事件A和B发生有时间差异,A先B后;在P(AB)中,事件A、B同时发生。
b、样本空间不同,在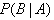 中,样本空间为A,事件P(AB)中,样本空间仍为Ω。
中,样本空间为A,事件P(AB)中,样本空间仍为Ω。
与“某校要组建篮球队,需要在各班选拔预备队员,规定投篮成绩一...”考查相似的试题有:
- 某单位招聘面试,每次从试题库随机调用一道试题,若调用的是类型试题,则使用后该试题回库,并增补一道类试题和一道类型试题...
- 自“钓鱼岛事件”,中日关系日趋紧张,不断升级.为了积极响“保钓行动”,学校举办了一场保钓知识大赛,共分两组.其中甲组满分...
- 在研究某新措施对“非典”的防治效果问题时,得到如下列联表: 存活数死亡数合计新措施13218150对照11436150合计24654300由表中...
- 甲乙丙三位同学独立的解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为、、,则有人能够解决这个问题的概率为A...
- 蒲丰(Buffon)投针问题:平面上画很多平行线,间距均为,向此平面投掷长为()的针,则此针与任一平行线相交的概率为 。
- 3个同学分别从a,b,c,d四门校本课程中任选其中一门,每个同学选哪一门互不影响;(I)求3个同学选择3门不同课程的概率;(I...
- 掷两颗骰子得两数,则事件“两数之和大于4”的概率为__
- 将一枚质地均匀的骰子抛掷一次,出现“正面向上的点数为6”的概率是( )A.13B.14C.15D.16
- 如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C.求:(Ⅰ)△AOC的面积小于32sin2π3的概率P1;(Ⅱ)△AOC为钝角三角形的概率...
- 在某项体育比赛中,七位裁判为一选手打出的分数如下:90 89 90 95 93 94 93去掉一个最高分和一个最低分后,所剩数据的方差为A...