本试题 “(1)选修4-4:坐标系与参数方程在曲线C1:x=1+cosθy=sinθ(θ为参数)上求一点,使它到直线C2:x=-22+12ty=1-12t(t参数)的距离最小,并求出该点坐标和最小距离...” 主要考查您对向量共线的充要条件及坐标表示
点到直线的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量共线的充要条件及坐标表示
- 点到直线的距离
向量共线的充要条件:
向量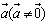 与
与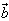 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得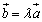 。
。
向量共线的几何表示:
设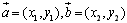 ,其中
,其中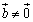 ,当且仅当
,当且仅当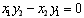 时,向量
时,向量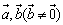 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: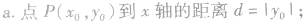
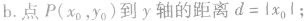
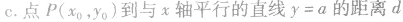

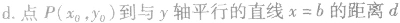
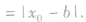
发现相似题
与“(1)选修4-4:坐标系与参数方程在曲线C1:x=1+cosθy=sinθ(θ...”考查相似的试题有:
- 直线与圆相交于M,N两点,若,则k的取值范围是_______________
- 若抛物线在点处的切线与圆(相切,则的值为_______.
- 若直线平分圆,则的最小值是A.1B.5C.D.
- 已知定点A(8,-6)、B(2,2),l为线段AB的垂直平分线.(1)求直线l的方程;(2)若x轴上的动点P到直线l的距离不超过1,求...
- 若点P在直线l1:x+y+3=0上,过点P的直线l2与曲线C:(x-5)2+y2=16相切于点M,则|PM|的最小值为( )A.2B.2C.22D.4
- 已知点M到双曲线x216-y29=1的左、右焦点的距离之比为2:3.(1)求点M的轨迹方程;(2)若点M的轨迹上有且仅有三个点到直线y=...
- (本小题满分12分)如图,设圆:,过原点作圆的任意弦,求所作弦的中点的轨迹方程.
- 经过点M(3,5)的所有直线中距离原点最远的直线方程是什么?
- 若椭圆(a>b>0)过点(-3,2),离心率为,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一...
- 已知圆,直线.(1)判断直线与圆C的位置关系;(2)设与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;(3)若定点P(1,1...